Eyelids
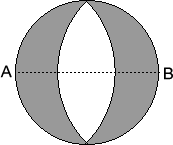
Can you work out the shaded area surrounded by these arcs?
Age
14 to 16
Challenge level
Problem
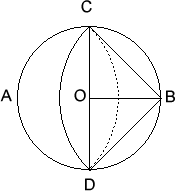
$AB$ is a diameter of a circle of radius 1 cm. Two circular arcs of equal radius are drawn with centres $A$ and $B$. These arcs meet on the circle, as shown. What is the shaded area?
Image
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Let $O$ be the centre of the circle and let the points where the arcs meet be $C$ and $D$ respectively. $ABCD$ is a square since its sides are all equal to the radius of the arc $CD$ and $\angle ACB=90^{\circ}$ (angle in a semicircle).
In triangle $OCB$, $CB^2 = OC^2 + OB^2$; hence $CB=\sqrt{2}$ cm. The area of the segment bounded by arc $CD$ and diameter $CD$ is equal to the area of section $BCD - $ the area of the triangle $BCD$, i.e.
$$\left(\frac{1}{4}\pi\left(\sqrt{2}\right)^2-\frac{1}{2}\times\sqrt{2}\times \sqrt{2}\right)\textrm{cm}^2$$,i.e. $(\frac{1}{2}\pi - 1)$ cm$^2$.
The unshaded area in the original figure is, therefore, $(\pi-2)$ cm$^2$. Now the area of the circle is $\pi$ cm$^2$, and hence the shaded area is 2 cm$^2$.
Image
