Efficient packing
How efficiently can you pack together disks?
Problem
How efficiently can you pack disks of the same size with no overlap? Imagine attempting to cover a 1m square with 10cm diameter disks with no overlap. What percentage of the area of the square can you actually cover using this obvious packing for disks?
Image
How much more efficiently would you be able to pack 1cm diameter disks into the 1m square? Could you make an estimate for the efficiency of packing disks of diameter 1mm?
- As a harder extension, make an estimate of the number of 1cm diameter balls that would be able to fit into a 1m cubed box.
Notes and background
Whilst it might seem relatively simple, the problem of 'shape packing' is often very difficult mathematically to solve with certainty for many shapes. Intuitive visualisation often works just as well as a strict mathematical analysis, and often is the only sensible possibility with packing together complicated shapes.
You might like to consider situations in which efficient shape packing is relevant in the physical world.
Student Solutions
First we need to find how many discs we can stack $1 \ \mathrm{m}$ in the $y$-direction, the centres of all the discs lie on a line at 60 degrees to the horizontal.
The total number stacked vertically $= \frac{1}{d\sin 60^\circ}$ (where $d$ is the diameter of a disc measured in m)
Case 1: $d = 10 \ \mathrm{cm} =0.1 \ \mathrm{m}$
$\textrm{Number of discs stacked vertically} = 11 $
$\textrm{Total number of discs} = (6 \times 10) + (5 \times 9) = 105 $
$\textrm{Packing fraction} = \frac{\textrm{No. Discs} \times \pi r^2}{1} = 0.825 $
Case 2: d=1cm = 0.01m
Number of discs stacked vertically = 115
Total number of discs = (58x100) + (57x99)= 11443
Packing fraction =$\frac{No. Discs x \pi r^2}{1}$= 0.899
Case 3: d = 1mm =0.001m
Number of discs stacked vertically = 1154
Total number of discs = (577x1000) + (577x999)= 1153423
Packing fraction =$\frac{No. Discs x \pi r^2}{1}$= 0.906
Extension
The most efficent method of packing spheres is face centred cubic packing, FCC packing will provide us with an upper limit to the number of spheres we can pack.
In the Face Centered Cubic (FCC) unit cell there is one host sphere at each corner and one host sphere in each face. Since each corner sphere contributes one eighth of its volume to the cell interior, and each face sphere contributes one half of its volume to the cell interior (and there are six faces), then there are a total of $\frac{1}{8}x8 + \frac{1}{2} x 6 = 4$ spheres in the unit cell.
Image
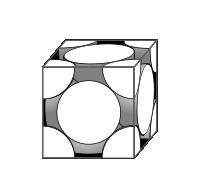
If we define
a = length of one side of the unit cell
r = radius of one sphere
we can see that 4rsin(45) = a.
The volume fraction of such a unit cell is the number of spheres in the cell multiplied by the volume of a sphere and then divided by volume of cube.
Volume fraction = $\frac{4x \frac{4}{3}\pi r^3}{(2\sqrt(2)r)^3}$ = 0.74
The number of spheres in a volume of $1m^3$ is therefore:
$\frac{0.74}{\frac{4}{3}\pi (0.005)^3}= 1413295$
This is the upper limit to the number of spheres we may pack. It is likely we will not actually be able to pack quite so many. If we did adopt this method we would have fractions of spheres along the sides of the container, as shown in the unit cell above.
Teachers' Resources
Why do this problem ?
This problem will allow students to engage with calculations of areas of disks, often used as an approximation to real objects in science. They will also practice visualisation skills.To find the best answer students will need to resort to trigonometry, although this is not necessary to make a satisfactory attempt at the question.
Possible approach
Whilst students might be familiar with the concept of the area of a disk they might be unable immediately to see how to apply this to the question in hand. Some discussion might facilitate this. Note that there are two 'obvious' different ways to pack disks. Which will work best? Discuss this. When they do the packing calculation, be sure to note that students must be clear as to exactly how may rows and columns of disks will fit into the grid. They can do this exactly (using trigonometry) or by drawing an accurate diagram and taking a measurement. Or, perhaps, they will produce some other valid method.Key questions
- Describe your method of packing the disks clearly in words.
- How many different sensible packing methods might you try?
- Can you be sure that each disk is completely contained within the confines of the square?
- What order of magnitude checks could you make to test that your answer is sensible?
Possible extension
Can students repeat the question by filling an equilateral triangle with side 1m?Possible support
Provide coins or counters for the students physically to work
with.
Students might struggle with the 'open' nature of the
questions. To begin, they might like to read the
Student Guide to Getting Started with Rich Tasks
