Double Cover
Weekly Problem 3 - 2007
What is the ratio of the area of the table covered twice, to the uncovered area?
What is the ratio of the area of the table covered twice, to the uncovered area?
Age
11 to 14
Challenge level
Problem
Image
A sheet of paper is exactly the same size as a rectangular table top. The paper is cut in half and the two halves are placed on the table as shown.
What is the ratio of the area of table left uncovered (white) to the area that is covered twice?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
We start by placing the two halves on the table so that the whole table is covered. Then we move them to overlap as in the question.
The area of the table covered by the paper has decreased by the two uncovered areas. The area covered by the paper has decreased by the amount covered twice. These two areas must both be the same, so the ratio must be $1:1$
Alternatively:
Image
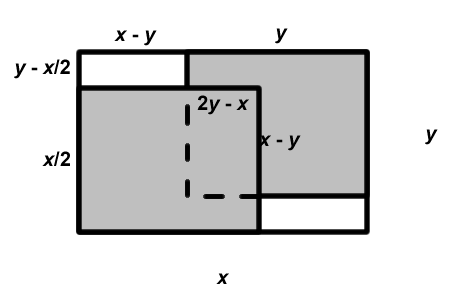
Let the sheet of paper have length $x$ and width $y$. Then the uncovered area consists of two congruent rectangles of length $x-y$ and width $y-\frac{1}{2}x$. So the uncovered area is $2(x-y)(y-\frac{1}{2}x)$, that is, $(x-y)(2y-x)$.
The area covered twice is a rectangle of length $y-(x-y)$, that is, $2y-x$, and width $\frac{1}{2}x-(y-\frac{1}{2}x)$, that is, $(x-y)$. So the area covered twice is also $(x-y)(2y-x)$.