Doodles
Draw a 'doodle' - a closed intersecting curve drawn without taking pencil from paper. What can you prove about the intersections?
Problem
A "doodle" is a closed intersecting curve drawn without taking pencil from paper. Only two lines cross at each intersection or vertex (never 3), that is the vertex points must be "double points" not "triple points". Number the vertex points in any order. Starting at any point on the doodle, trace all the way around the doodle (following the path you originally drew, forwards or backwards) until you get back to where you started. Write down the numbers of the vertices as you pass through them. So you have a [not necessarily unique] list of numbers for each doodle.
Prove that
- each vertex number in a list occurs twice. [ easy ! ! ! ]
- between each pair of vertex numbers in a list there are an even number of other numbers [ hard ! ! ! ]
Student Solutions
James cracked this toughnut for
us:
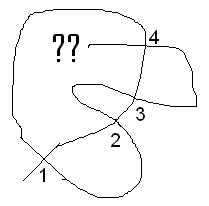
To prove that each vertex number in the list twice, I noticed
to get back to where we started pointing in the same direction we
started we must go fully around the curve. So we will cover the
entire curve, and since the curve goes through each vertex twice,
the number of each vertex will appear twice.
For the next part, I tried to doodle with an odd number of
vertex number between the pair:
Image
As expected, I ran into some problems. If we consider the
number between the pair of 1's. Going around anti-clockwise 2
crosses, then 3, then 4, and so on. If there are an odd number of
crosses then the end of the line will end up inside the loop. But
it can't cross this line again, and so we will always have one end
of the line stuck inside the loop, and one outside, and so the
curve couldn't be closed.
So between every pair we must have an even number of vertex
numbers (since any pair will form a loop similarly to above).
