Dividing a cake
Problem
On Annie's ninth birthday her Mum made her a cake which had the figures from $0$ to $9$ round the edge in red icing instead of candles.
Starting from the centre, Annie cut the cake into $3$ pieces with $3$ cuts so that the numbers on each piece added to the same total.
Where were the cuts and what fraction of the whole cake was each piece?
Getting Started
It might be easier to work from this picture of the top of the cake with all possible cuts marked:
You will find two copies of the cake top marked like this on this sheet.
What do all the numbers $0$ to $9$ add to? So what will the numbers on each of the three pieces add to?
Student Solutions
Again, we received lots of solutions to this problem, but not many of you answered everything!
Alice, Gwen, Amber and Emma from The Downs C.E.P. School began by trying to divide the cake into equal sized pieces. They described how they soon found that the numbers didn't add up to the same total. They discovered another strategy which Serena and Philippa at Brighton College Prep School explain well:
Step $1$
Add up all the numbers on the cake. They should equal $45$.Step $2$
Divide the number by 3 because that is how many pieces of cake they want.Step $3$
Add up three sets of numbers that equal $1$5. You should have:
i) $9 + 0 + 1 + 2 + 3$
ii) $6 + 5 + 4$
iii) $8 + 7$
Many of you used this idea including Lewis and Emma from St
Mary's RC School and Anders at Bentley Park College.
Jennifer from Crownfield Junior School tells us exactly how she did
it:
At first I had no idea how to work it out. I was sitting there telling my mum every thought or question I had about it, and then it came to me. I went online to the Nrich website to find a clue. Once I had answered the clue, which was a question, I knew exactly how to work it out.The answer was $45$, so as we had to cut the cake into three pieces. I divided $45$ by three. My answer was $15$. Therefore each piece would have to add up to $15$. I sat there making $15$ and finally I got it. I wasn't $100$% sure so I checked with my mum. Fortunately she told me I was correct.
I have only one piece of advice for anyone attempting to solve this problem that is stay calm and tell someone every question or thought you have about the problem.
Excellent advice Jennifer, thank you!
Many more of you sent correct solutions like Sam from
Congerstone Primary School.
Cansu, Gur, Burak, Koray and Kaan from Mef School in Turkey sent us
the answer pictorially:
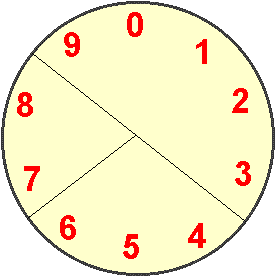
Add up how many numbers there are = $10$
There are $5$ numbers on the first piece of cake = ${5\over10}$ (or ${1\over2}$)
There are $3$ numbers on the second piece of cake = ${3\over10}$
There are $2$ numbers on the third piece of cake = ${2\over10}$ (or ${1\over5}$)
