Distinct in a Line
This grid can be filled so that each of the numbers 1, 2, 3, 4, 5 appears just once in each row, column and diagonal. Which number goes in the centre square?
Problem
Image

The grid can be filled up using only the numbers 1, 2, 3, 4, 5 so that each number appears just once in each row, once in each column, and once in each diagonal.
Which number goes in the centre square?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
$3$, $4$ and $5$ are on diagonals, so can't go in the centre square (since each number must appear just once on each diagonal).
So the number in the centre square must be a $1$ or a $2$. Suppose it was a $1$. Then we must put $1$s as shown in red:
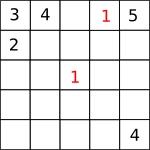
and $2$s as shown in blue:

So there must be a $1$ in place of one of the crosses:
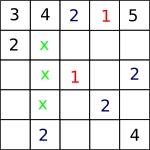
But the top and bottom cross couldn't be $1$, since they are on the diagonal, and the middle cross can't be $1$ since it's on the $3$rd row (where there's already a $1$). So $1$ can't go in the centre square after all!
$2$ goes in the centre square.
Alternatively, consider the bottom-left corner. $2$ and $3$ are in the same column, $4$ is in the same row and $5$ is in the same diagonal. Therefore, this must contain a $1$.
Then, the centre is in the same diagonal as each of the corners, so cannot be $1$, $3$, $4$ or $5$. This means the centre must contain a $2$.
So the number in the centre square must be a $1$ or a $2$. Suppose it was a $1$. Then we must put $1$s as shown in red:
Image

and $2$s as shown in blue:
Image

So there must be a $1$ in place of one of the crosses:
Image

But the top and bottom cross couldn't be $1$, since they are on the diagonal, and the middle cross can't be $1$ since it's on the $3$rd row (where there's already a $1$). So $1$ can't go in the centre square after all!
$2$ goes in the centre square.
Alternatively, consider the bottom-left corner. $2$ and $3$ are in the same column, $4$ is in the same row and $5$ is in the same diagonal. Therefore, this must contain a $1$.
Then, the centre is in the same diagonal as each of the corners, so cannot be $1$, $3$, $4$ or $5$. This means the centre must contain a $2$.
