Different deductions
There are lots of different methods to find out what the shapes are worth - how many can you find?
Problem
If you are a teacher, click here for a version of the problem suitable for classroom use, together with supporting materials. Otherwise, read on...
Each symbol has a numerical value. The total for the symbols is written at the end of each row and column.
Can you find the missing total that should go where the question mark has been put?
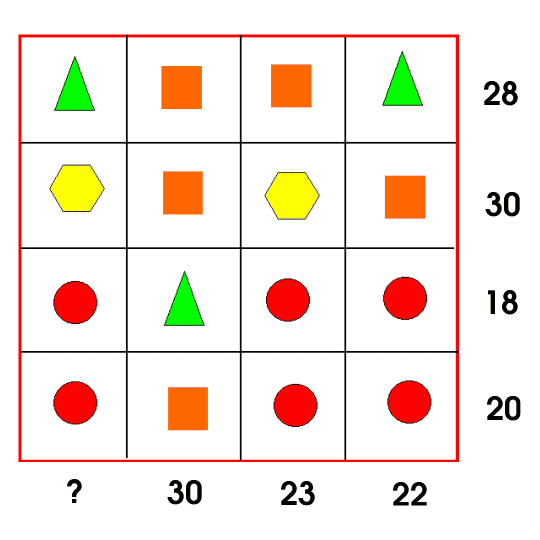
Image description
For accessibility: A grid of triangles T, squares S, hexagons H, and circles C.
From left to right, top to bottom, the grid reads: T, S, S, T; H, S, H, S; C, T, C, C; C, S, C, C.
The totals for the rows from top to bottom are: 28, 30, 18, 20.
The totals for the columns from left to right are: ?, 30, 23, 22.
There is a lot of information in the grid, so you will need to make some choices about what to focus on first. Click below to see some images that draw your attention to particular parts of the grid.
What can you deduce from each image?
Image 2
Image 3
Image 4
Image 5
Image 6
Getting Started
What can you deduce by comparing the bottom two rows?
If you could work out the value of the square, how could you then work out the value of the triangle?
Student Solutions
We had quite a few solutions submitted for this task.
Oliver, Nicholas, Hayden, Elena and Iris, Jasmine and Dylan, Christie and Natalie from Peak School in Hong Kong said they mostly used 'guess, check and improve' to find the different values.
Henry from Winterfold House School sent in the following:
We chose a row that had three of the same shapes. We selected the highest FACTOR of the total for that row in place of the shape. Assuming the second shape was the difference between 3 times the first shape, we began to test and refine our solution using the other lines, columns and totals. circle=4; square=8; triangle=6 and hexagon=7
Tri from the British Vietnamese International School wrote:
This question is not hard or easy. My solution is to look at the first horizontal line and the two vertical lines from the right. You can see that:
2 square+ 2 triangle = 28, 3 square+1 triangle= 30.
You can say that the difference between 1 square and 1 triangle is 2.
So we have 28-2-2=24 because to make all the shape equal, 24 = 4 triangle so 1 triangle=6 and 1 square=8.
Now we can look at line 3 and 4 horizontal and we can see that 20 = 8 + 3c so circle = 4 and at line 3 vertically, we can have 23-4-4-8=7. so the? equals 7+4+4+6=21
Zara and Felicity from North London Collegiate Junior wrote:
In Maths Mayhem, our after-school maths club we solved this problem.

Kavisin and Akshaya from Athelney Primary School wrote:
We worked this out in a systematic way. This is how we solved it:
We subtracted shapes and got some answers by looking at the totals of each column and row. We want to see if the numbers are greater or less than others. Then we knew that 2 squares plus 2 triangles = 28 and that means a square add a triangle = 14. We worked out that the difference between them was two and 14 -2 = 12. 12 divided by 2 is 6 so the triangle = 6 and the square = 8. When we knew that we worked out the other shapes and finally we found out the mystery number is 21!!!
Triangle plus Hexagon plus Circle plus Circle =21. 6 + 7 + 4 + 4 = 21
Freda from Meavy School sent in the following:
I found out that a square is two more than a triangle. Then I worked it out from there that a square must be 8 and a triangle must be 6. I then worked out a circle was 4 because there was a gap of 8, and there were two circles in the line. Finally, I looked at the value of a hexagon. I worked out that I needed 14 more to make the line with 2 hexagons and 2 squares. I knew that the 2 squares made 16 so that left 14 for the 2 hexagons. I split 14 and it made 7.
The final line was 7+6+4+4= 21.
Fred from Harris Primary Academy Shortlands said:
I started with the "30" column. This column has the same shape three times and one different shape. It adds up to 30. I thought "what number goes into 30 three times with a bit left over?" First I tried 9 for the orange square and 3 for the green triangle: 9+9+9 = 27, 27 + 3 = 30. Then I filled in the numbers that occurred there everywhere else. I tested it with the top row which adds up to 28. 3 + 9 + 9 + 3 = 24. So that can't be right!
Then I went back to my original column and tried some different numbers. 8+8+8 = 24, 24 + 6 = 30. So 8 and 6 would also work. I tried 8 and 6 in the top row and it worked: 6+8+8+6 = 28!
Once I had done this I could work out the bottom two rows with the red circles. The circle is worth the same in both rows, the only difference is that one row has a green triangle and one has an orange square. For the bottom row, I took away the number I already knew from the total: 20-8 = 12. I knew that 3 circles = 12 so 12 divided by 3 gives you one circle be 4.
Once you have three of the shapes you can work out the last one by adding down in the 23 column and working out what's left.
To get the answer I added all the answers to the shapes together. 6 + 7 + 4 + 4 = 21.
So the answer is 21.
Holy Trinity Pewley Down School sent in 3 solutions:



Florence from Walthamstow Hall Junior School wrote the following and there were other solutions from Gabby and Melissa:
I started off by seeing what value some shapes had compared to others. The one you need to find out is the comparison between the square and the triangle. You can find this out by using the top 3rd and 4th rows or the top row and the 2nd column. For using the top row and the 2nd column: If 2 triangles+2 squares = 28. 1 triangle+3 squares= 30
When you substitute one of the triangles for a square, the total increases by 2. This means that 1 square must be 2 more than a triangle.
For using the 3rd and 4th rows: If 3 circles + a triangle = 18, And 3 circles + a square = 20
When you substitute the triangle for a square, the total increases by 2. This means that 1 square must be 2 more than a triangle.
Now you know that 1 square is 2 more than a triangle, this is how to figure out the exact value of the square and the triangle:
Again you use the top row and the 2nd column.
You know that 1 triangle + 3 squares = 30, so if you turn the triangle into a square by adding 2, the equation becomes 4 squares = 32. To find the value of a square, you divide 32 by 4 to make 32 ÷ 4 = 8. This means that a square's value must be 8. (To check this you can substitute two triangles into circles on the top row.)
Now that you know the value of a square and that a triangle is 2 less than a square, to find the value of a triangle you can do 8 - 2 = 6. Again you can check that this is correct by substituting shapes for numbers on the rows that only use squares and triangles.
To find the value of the remaining two shapes:
There are many ways to now find the value of the hexagon and the circle. The most obvious one is to:
1st use the 3rd and 4th rows to find the value of the circle.
If 3 circles + a square (8) = 20, just subtract the 8 from the 20 to make 20 - 8 = 12 and 12 ÷ 3 (representing the 3 circles) = 4. This 4 must be the value of a circle. (To check you can use the third row with a triangle rather than a square.)
To find out the value of a hexagon: (this is the easiest way, there are others)
Use the 2nd row. 2 squares + 2 hexagons = 30. 30 - 16 (2 squares) = 2 hexagons = 14
14 ÷ 2 (representing the 2 hexagons) = 7. This means that the value of a hexagon must be 7.
Overall values: Square = 8; Triangle = 6; Circle = 4; Hexagon = 7.
To find the missing value: A triangle + a hexagon + 2 circles = 6 + 7 + 4 + 4 = 6 + 7 + 8 = 21.
The missing value/answer is 21.
Thank you all for your contributions.
Teachers' Resources
Why do this problem?
This problem provides a fantastic opportunity for learners to articulate their reasoning and could introduce them to the idea of redundant information. It is also offers a context in which to become familiar with the idea of a symbol representing an unknown quantity which is a key idea in algebraic thinking. (If you are using this task with older students, beyond the primary age range, you may wish you look at the secondary version of these notes.)
Drawing attention to particular parts of the grid makes different ways of approaching this task explicit. Giving children the chance to discuss these different methods means they can add them to their mathematical 'toolkit' and encourages them to be more resilient mathematicians, shifting the focus away from the answer to the journey towards a solution.
Possible approach
Display this grid on the screen for everyone to see:
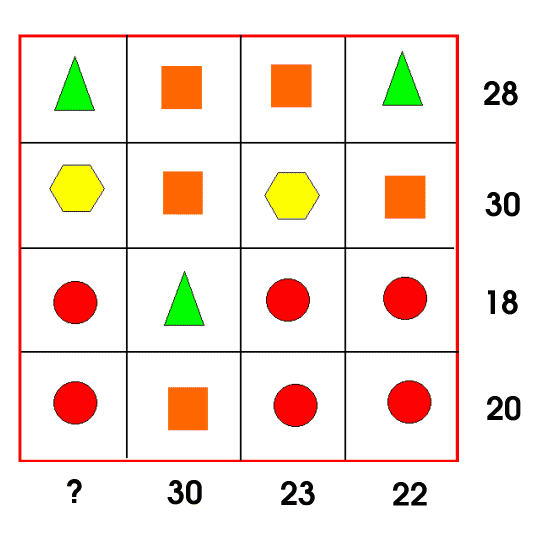
Allow a few minutes for children to look at the image and consider what they see. Suggest that they share ideas with a partner before taking some comments as a whole group. Invite anyone in the room to respond and use this process to 'set the scene'.
Pose the problem orally, and/or by handing out this sheet, or displaying this PowerPoint slide. Explain that this is a particularly interesting problem because it can be solved in lots of different ways. Give pairs time to begin to tackle the task, but after a few minutes, hand out this sheet, containing six different images, suggesting different starting points. The images are also available on these PowerPoint slides.
Reassure the group that there is a lot of information in the grid, so they had to make some choices about what to focus on first. Explain that each image on the worksheet draws attention to particular parts of the grid. What can they deduce from each? How can each help them to solve the problem?
Warn everyone that in a while, you're going to invite pairs up to the board to explain how they would use a chosen image to find the missing total. (The worksheet is set out so if you don't want everyone to work on every image, you can give half the class the odd numbered images and half the class the even numbered images.)
Allow time for pairs to work and, as they do so, circulate round the room, listening for examples of clear reasoning. After ten minutes or so, it might be appropriate for you to group together two pairs who have been working on the same image so that they have chance to talk as a four about how they used the image, and to rehearse their reasoning.
In the plenary, encourage these groups of four to explain their reasoning, giving the rest of the class the opportunity to chip in and ask questions. You could also invite any pair who had created their own different approach to tall the whole class about it.
Ideally, in a follow-up lesson, you could use the Fruity Totals interactivity to generate other versions of the same problem so that learners have the opportunity to practise the methods.
Key questions
If you could work out the value of the square/hexagon/circle/triangle, how could you then work out the value of the triangle/circle/hexagon/square?
What can you deduce by comparing (for example) the bottom two rows?
Possible extension
Using the Fruity Totals interactivity, can students work out how much information is necessary to solve the problems uniquely, and identify redundant information?
Possible support
The problem could be solved by trial and improvement, so suggest students choose a value for a particular shape and explore the consequences. While this strategy makes the task accessible, by sharing different methods, the idea is to move learners on to more sophisticated approaches.
