Difference Sudoku
Use the differences to find the solution to this Sudoku.
Problem
Difference Sudoku printable worksheet
By Henry Kwok
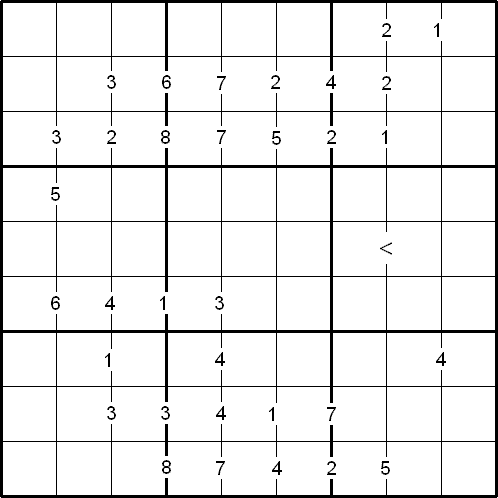
Rules of Difference Sudoku
Like the standard Sudoku, the object of the puzzle is to fill the whole $9 \times 9$ grid with numbers from $1$ to $9$, so that each row, each column, and each of the nine $3 \times 3$ squares contain all nine digits.
There are special clue-numbers placed on the border lines between selected pairs of adjacent squares of the grid. Each clue-number is the difference between the two numbers in the adjacent squares.
For example, a clue-number $7$ on the border line between two adjacent squares means that the possible pairs of numbers for the squares on either side must be one of the following combinations: $1$ and $8$, $8$ and $1$, $2$ and $9$, or $9$ and $2$.
The inequality sign indicates that the number in row 5 column 7 is smaller than the number in row 5 column 8.
As this variant has only one inequality sign on the border line, it is called Minimal Difference Sudoku.
Getting Started
If you can manage to reduce the possibilities of one cell to 2 or 3 numbers, you could try solving the puzzle with each of those values in turn. If you reach a contradiction (for example a number is repeated in a row, column or square) then you can rule out that value and try one of the others instead.
Here's an example of a way to start this puzzle. Let's look at this section of the grid:

We need two numbers that differ by 8, they can only be 1 and 9.
But which way round should they go?
Let's try both possibilities, writing one pair at the top of the cells and the other at the bottom:

Then we can use the '7' to determine the value of the next cell for each of our possibilities:

We can keep going in this way with two possible solutions emerging until one of them ends in a contradiction.
Rosie and Zoe solved this Sudoku. They kept a record of the order in which they filled the Sudoku and wrote it in the boxes. Their journey can be found here. This is just one possible route through the problem.
Student Solutions
We received correct solutions from Cynthia and Lindsay from NLCSJeju, Jemma from Twynham School, and Lee from Lucton School.
Well done everyone! Here is Jemma's solution:.pdf
Jemma gave this explanation of how she solved the puzzle:
When I first looked at the difference Sudoku, I recognised that there were a few boxes where there was only one possible answer ( the ones with an eight difference); you just didn't know which way round the numbers went. I found all of them, and experimented with them until I thought they were mostly right. I then worked on the bottom two lines as it gave you the most information for those two lines. I worked out the possible pairs and filled those two lines with the numbers 1-9 only once. Once I finished those two lines, I worked on the second and third rows to the top. Once I had filled them in, so it worked horizontally and vertically, I decided to try and finish the top row (to complete the top three boxes). That really helped me and allowed me to try and complete the rest of the difference Sudoku. Once I was finished, I looked back at my work and spotted one mistake; however, that could be easily fixed as all I had to do was switch two numbers round at the top, and switch two numbers round in the middle. I checked it, and didn't find any more mistakes.
