Diagonal trace
Problem
A pentagon has five diagonals (lines drawn between the corners). You can trace over all of the diagonals without lifting your pencil and without going over any more than once. Try it.
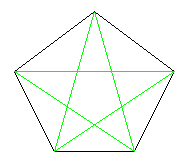
Can the same thing be done with a hexagon (6 sides) or with a heptagon (7 sides)?
(Take care to find ALL the diagonals. Drawing a large shape will help.)
Getting Started
It might help to draw in all the diagonals first, then trace over them with a coloured pencil.
You could print off this sheet which has the shapes and the diagonals drawn for you.
Do you have some sort of system for trying to trace over the diagonals?
Student Solutions
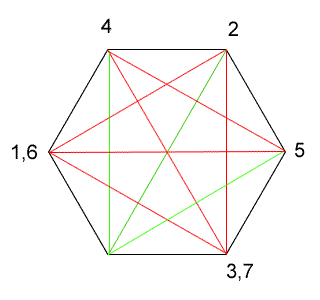
You will have found that it is impossible to trace over all of the diagonals of a hexagon without going over the same line twice. Why is this? The trick is to look at how many diagonals are connected to each vertex. Jenni offers us a very clear explanation:
Each time you draw a line IN to a vertex, you also need to have another line going OUT (unless you are on the end point). If there is an even number of lines, then you will always be able to go in and out of any vertex without using the same line twice. However, if you have an odd number of diagonals connected to each vertex, then sooner or later you will revisit a vertex and find that there are no more available lines going out of it.
The diagram below shows all the diagonals available in a hexagon. The red lines show one possible path, and the numbers show the order in which I visited the vertices. As you can see, when I get back to vertex 3/7, there are no more lines going out of the vertex that haven't been used yet (these would be shown in green). This would happen whichever path you took - eventually you would have to return to a vertex for a second time and there would be no way out.
Now let's look at the heptagon. By drawing all the possible diagonals as before, you will see that there are now fourlines connected to each vertex. Because this is an even number, there will always be the same number of lines IN to a vertex as there are OUT, so you will never get stuck. The only time you will revisit a vertex for the third time is when you return to the one you started with, but then you have completed the task. Follow through the numbered path indicated on the diagram:
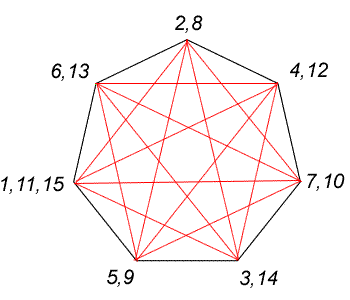
Thank you, Jenni.
Can you see that this will always be possible for shapes with an odd number of sides, because they always have an even number of diagonals connected to each vertex? On the other hand it would never be possible for any shape with an even number of sides, for the opposite reason.
