Cut it out
Can you dissect an equilateral triangle into 6 smaller ones? What number of smaller equilateral triangles is it NOT possible to dissect a larger equilateral triangle into?
Problem
An equilateral triangle can be dissected into four (equal) smaller equilateral triangles.
Can you dissect an equilateral triangle into six smaller ones, not necessarily all the same size?
Is it possible to dissect a larger equilateral triangle into any number of smaller equilateral triangles?
Are there any numbers that are impossible?
Getting Started
What is the smallest number of triangles you can break one triangle in to?
You could print out this sheet of triangles or use isometric dotty paper.
Student Solutions
The diagram shows an equilateral triangle dissected into 4 smaller equilateral triangles. Which numbers of smaller triangles are possible and which are not, and why? This remains a Tough Nut as nobody has yet explained why it is impossible to dissect an equilateral triangle into certain numbers of smaller equilateral triangles.
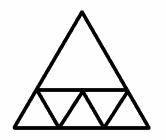
Robert and Andrew, St James Middle School, Bury St Edmund's sent this solution with six equilateral triangles. They say they think this is the only solution with 6 smaller triangles other than rotating the shape.
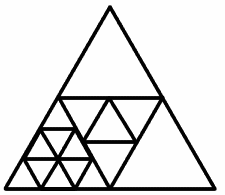
Talei and Stephanie of Poltair Community School and Sports College, St Austell, Cornwall said they think that dissection into 2 or 3 smaller triangles is impossible and that 4 is the smallest number of triangles possible. They gave this as an example of dissection into 15 smaller triangles.
Talei's also had the idea of allowing overlapping triangles and realised that this would make it possible to have any number of smaller triangles, even infinitely many, but that would be a different question.
Lucas from St. Joseph's in Reading wrote in this wonderful explanation.
It is possible to make any number of smaller triangles except 2, 3 and 5 in the large equilateral triangle. Any even number can be made by drawing an odd number of small triangles in a row along the bottom going up, down, up, therefore creating a larger triangle on the top. For odd numbers ( This works for even numbers above 9), simply subtract 3 from that number - for 7 we would get 4 - Have you made this triangle yet? If not, subtract 3 again and so on. In the number 4 triangle (Or whichever you are using), find a smaller triangle, pointing up or down, and inside of it draw a triangle pointing in the opposite direction with the corners touching the sides. Count up the triangles and you should find that there are the number you are looking for. This is because a triangle has 3 sides, so as well as the triangle in the middle, it creates 3 around the edge.
Teachers' Resources
Cut it Out
An equilateral triangle can be dissected into four (equal) smaller equilateral triangles.
Can you dissect an equilateral triangle into six smaller ones, not necessarily all the same size?
Is it possible to dissect a larger equilateral triangle into any number of smaller equilateral triangles?
Are there any numbers that are impossible?
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support