Cushion ball
Problem

A standard English snooker table is 6' x 12'. We know that the shortest path between any two points on the table is given by the straight line between them. How do we figure out the shortest distance between two points if the ball must bounce off one wall? What if it must bounce off 2 walls? 3 walls?
If you want to try one yourself, let the bottom left hand corner of the pool table be the origin. Consider the case when the cue ball is at (5,5) and the target ball is at (10,2). Which wall gives the shortest path to the target?
Getting Started
If you draw copies of the table reflected in the cushions then the reflection of the path of the ball after hitting a cushion appears as a straight line in the image of the table.

Student Solutions
You might like to refer to some of the ideas in the Plus issue 10 article, In space, do all roads lead to home?. It's all done with mirrors!
Jon Farradane supplied the following solution:
For an n-bounce route, find the nearest 'n-times reflected' image of one point as viewed from the other, using a mirror boundary. The ray path gives the solution. Jon says this works only for a boundary made of straight edges.
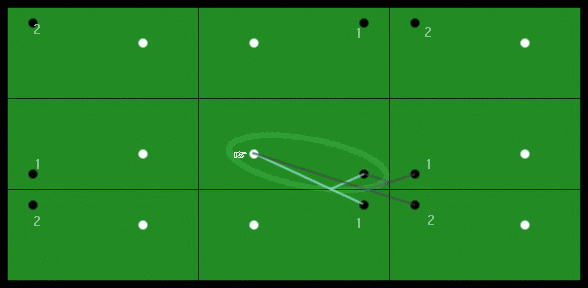
Jon also supplied a slightly more complex method which solves the 1-bounce problem and works better if you wish to take advantage of the curved areas of the table edge around the pockets. He suggests investigating the family of ellipses which have their foci at the two balls. The ellipse with the highest eccentricity that makes a tangent to the cushion will touch it at the bounce point for the shortest route.
Jon also raised the question of how to solve the problem for circular tables. The ellipse technique still works, but it's not an easy problem to solve analytically!
Teachers' Resources
Why do this problem?
The context is interesting and this can be an exercise in finding distances using coordinates. This process, of repeatedly reflecting the snooker table in its sides, occurs in many areas of advanced mathematics and for a simple introduction see the article In Space Do All Roads Lead Home?
Possible approach
Use the hint.
Key question
We know the ball bounces of the cushion at an equal angle so how do we use this fact to find the right point on the cushion to aim for?
Possible support
See Snookered.
