Concrete wheel
Imagine that you are sitting in a room at ground level, facing a floor-to-ceiling window which is 20 feet by 20 feet.
A huge concrete wheel, 100 miles in diameter, is rolling down the street and is about to pass right in front of the window, from left to right.
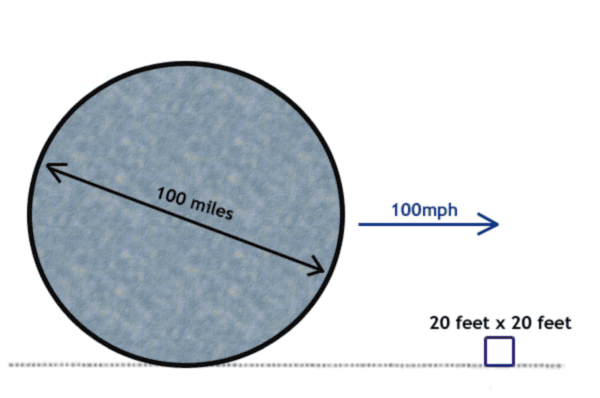
The centre of the wheel is moving to the right at 100 miles per hour.
What does the view look like, from inside the room, as the wheel passes by?
This problem appears in "Mathematical Thinking and Problem Solving", edited by Alan Schoenfeld and published by LEA press.
Alan Schoenfeld reports that:
Some people think that the room will go (almost) instantaneously dark as the wheel first passes the window, that it will stay dark for a short while and then go (almost) instantaneously light as the wheel leaves.
Others think that the room will go (almost) instantaneously dark as the wheel first passes the window, that it will stay dark for a relatively long time and then go (almost) instantaneously light as the wheel leaves.
Others think that the room darkens slowly, as though a large curtain is being pulled, more or less horizontally (from left to right), or diagonally (from the top left corner), or vertically downwards, as in the sketches below: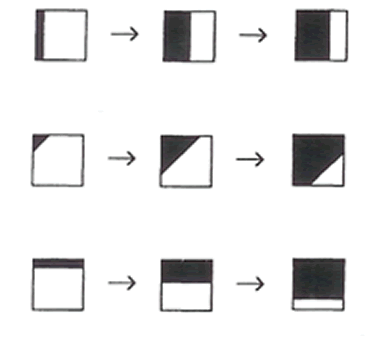
The room then stays dark for a short /long period of time, after which it lightens in a way that is complementary to the way it darkened.
What do you think?
Well done to everyone who correctly worked out that the third solution in the hint is correct. From 20 feet above the ground the bottom of the wheel appears horizontal, so it covers the top right corner almost immediately after covering the top left corner.
Thanks to Julian (Hastingsbury School) who worked out how long the window would be covered for.
If you consider the radius that touches the ground, the angle this makes with the radius 20 feet above the ground is 0.7 degrees, so the wheel turns 1.4 degrees whilst covering the window.
The wheeil travels 100pi miles each time it completes a whole turn, taking pi hours. So the wheel will cover the window for (1.4 / 360) pi hours = 0.0122 hours = 44 seconds. The angle of the tangent to the circle where it first touches the window is less than 1 degree to the horizontal, and so it appears to be coming down horizontally as we expected above!
Alan Schoenfeld suggests that this problem tends to provoke immediate and widely divergent intuitive reactions (see some of the possibilities listed in the Hint section).
He writes that he used this problem in a class where the discussions "focused on what it means to have a compelling mathematical argument. The general tenor of these discussions followed the line of argumentation outlined in Mason, Burton and Stacey's (1982) Thinking Mathematically : First, convince yourself; then, convince a friend; finally, convince an enemy. (That is, first make a plausible case and then buttress it against all possible counterarguments.) In short, we focused on what it means to truly understand, justify, and communicate mathematical ideas."
Teachers may want to use this problem in their classrooms to serve the same purposes.