Colouring Triangles
Explore ways of colouring this set of triangles. Can you make symmetrical patterns?
Problem
What do you see below?


What do you notice?
What is the same and what is different about the two pictures?
Now, it is your turn to colour!
Explore ways of colouring the black and white outline of the triangles:

Can you make symmetrical patterns? With two colours? Three colours?
More than three colours?
You may like to use the interactivity below to try out your ideas. This sheet of blank triangles might also be useful.
We would love to see the triangles you create. Do send them in along with your explanation of how you know the pattern is symmetrical.
Getting Started
You might find it useful to print off this sheet of lots of the triangles.
How do you know your design has a line of symmetry?
Have you tried using more/fewer colours?
Student Solutions
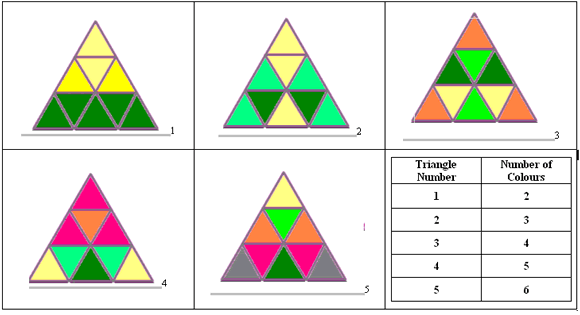
Kesavan from Latymer All Saints C of E Primary sent the following designs, which all have a vertical line of symmetry:
Rayyan from Doha College in Qatar sent in the following:
I know that my triangle is symmetrical because when you fold it in half vertically, both sides are exactly the same. Another way of showing this is putting a mirror on the line of symmetry. If you look at it from one side, it will look the same as the normal triangle.

Shawn from Lanesborough School in Surrey sent in a picture.

Well done for producing these triangles with symmetry, perhaps there are more that others could find.
Teachers' Resources
Why do this problem?
Possible approach
You can then set them off on the activity. Pairs would benefit from access to the interactivity on a computer, laptop or tablet as this allows them to try out ideas and easily tweak them. Having a copy of this sheet of the two coloured triangles to refer to, and this sheet of blank triangles to record their designs, would be helpful.
After a little while, give each pair time to share their designs with another pair so the four children together confirm that each way of colouring does indeed have line symmetry.
Key questions
Where is the line of symmetry in this design?
Possible extension
Alternatively, can learners colour the small triangles, using four colours, with no two triangles of the same colour side-by-side?
