Circumspection
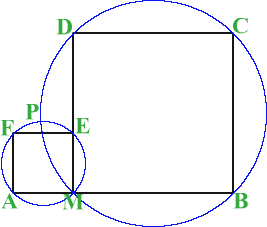
M is any point on the line AB. Squares of side length AM and MB are
constructed and their circumcircles intersect at P (and M). Prove
that the lines AD and BE produced pass through P.
Age
14 to 16
Challenge level
M is any point on the line AB. Squares of side length AM and MB are constructed and their circumcircles intersect at P (and M).
Prove that the lines AD and BE produced pass through P.
Image
Look for angles which will help you to show that the angles in question are $180^{\circ}$ so the lines are straight.
M is any point on the line AB. Squares of side length AM and MB are constructed and their circumcircles intersect at P (and M).
Pick up a pencil, do some drawing, play with this. Look at angles APM, MPD, AEM, MCD and look for cyclic quadrilaterals. The proof that the lines AD and BE produced pass through P takes three or four lines.