The circle of Apollonius... coordinate edition
Can you sketch and then find an equation for the locus of a point based on its distance from two fixed points?
Problem

This resource is from Underground Mathematics.
Two fixed points $A$ and $B$ lie in the plane, and the distance between them is $AB=2a$, where $a>0$.
A point $P$ moves in the plane so that the ratio of its distances from $A$ and $B$ is constant:
$$\frac{PA}{PB}=\lambda,$$
where $\lambda>0$.
- Can you sketch the locus of the point $P$ for different values of $\lambda$?
- Using Cartesian coordinates, work out (the equation of) the locus of $P$.
Suggestion
You may find it more straightforward to first work with specific values of $a$ and $\lambda$, say $a=2$ and $\lambda=3$.
Part 2
Now assuming that $\lambda\neq1$, find the radius and centre of the circle. What is the length of the tangent to this circle from the mid-point of $AB$? What shape is traced by the tangent as $\lambda$ varies?
Background
This circle is known as the circle of Apollonius, named after the Greek geometer Apollonius of Perga.
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Student Solutions
Thanks to Jordan from St Stephen's School, and Elin for submitting solutions to this problem.
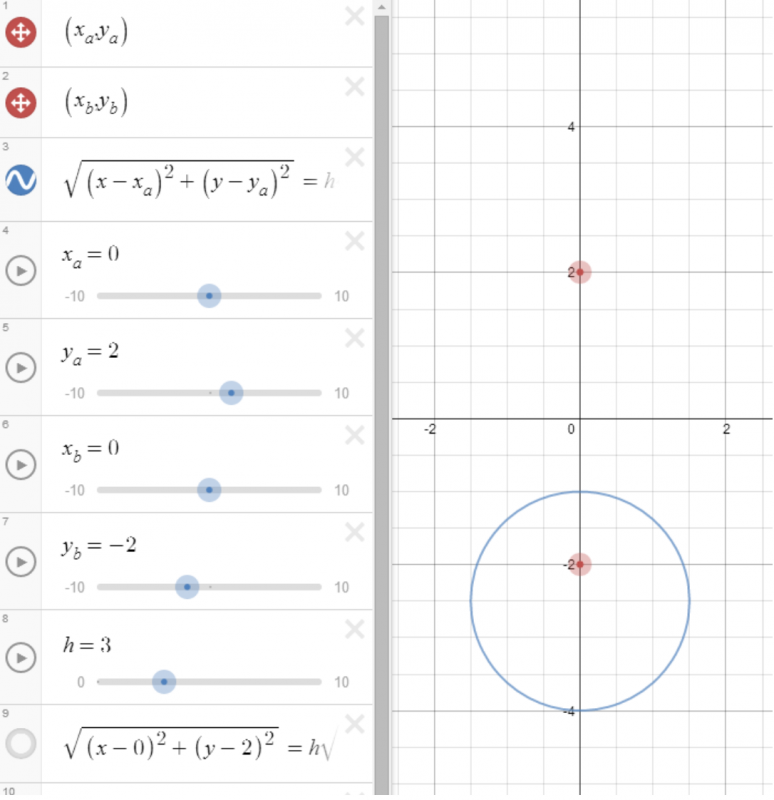
Jordan started off by using Desmos to plot the locus of P in various cases:
Assume $ \lambda=3 $ and $a=2$. Let A be the point $(0,2)$ and B be the point $(0,-2)$.
Then the equation for the locus of P can be written:
$$\sqrt{(x-0)^2+(y-2)^2}= 3 \sqrt{(x-0)^2+(y+2)^2}$$
When plotted in Desmos this gives a circle which looks like this:
Desmos also allows the use of sliders so it is possible to explore different values of $\lambda$.
Below are plots for $\lambda=2$ and $\lambda=0.5$ in red:
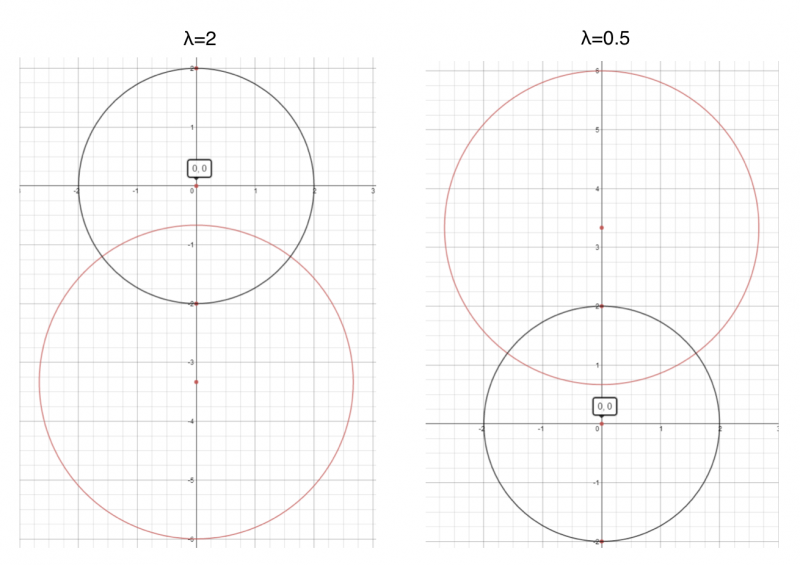
We observe that in both cases it gives a circle but when $\lambda=2$ the circle contains the point A and when $\lambda=0.5$ the circle contatins the point B.
In Elin's solution she has rearranged the equation for the locus of P so that it is in the standard form of the equation of a circle:
Let A be the point $(0,0)$ and B be the point $(0,4)$.
(It doesn't matter that Elin has used different points A and B to Jordan, all that matters is that the distance between A and B is 4. It does however mean that Elin's initial equation is slightly different, but it is arrived at in the same way)
Then the equation of the locus of P is:
$\sqrt{(x-0)^2+(y-0)^2}= 3 \sqrt{(x-4)^2+(y-0)^2}$
$x^2+y^2= 9((x-4)^2+y^2)$
$x^2+y^2= 9(x^2-8x+16+y^2)$
$x^2+y^2= 9x^2-72x+144+9y^2$
$ 8x^2-72x+144+8y^2=0$
$ x^2-9x+18+y^2=0$
$ (x-9/2)^2-9/2^2+18+y^2=0$
$ (x-9/2)^2+y^2=9/2^2-18$
$ (x-9/2)^2+y^2=9/4$
Hence the locus of P is a circle with centre $(\frac{9}{2},0)$ and radius $\frac{3}{2}$.
Elin has also done the same in the general case where $a$ and $\lambda$ are not fixed
Let A be the point $(0,0)$ and B be the point $(0,2a)$.
Then the equation of the locus of P is:
$\sqrt{(x-0)^2+(y-0)^2}= \lambda \sqrt{(x-2a)^2+(y-0)^2}$
$x^2+y^2= \lambda^2((x-2a)^2+y^2)$
$x^2+y^2= \lambda^2(x^2-4ax+4a^2+y^2)$
$x^2+y^2= \lambda^2 x^2-4a\lambda^2 x+4a^2\lambda^2+\lambda^2 y^2$
$ (\lambda^2-1)x^2-4a\lambda^2 x+4a^2\lambda^2+(\lambda^2-1)y^2=0$
$ x^2-\frac{4a\lambda^2}{\lambda^2-1}x+\frac{4a^2\lambda^2}{\lambda^2-1}+y^2=0$
$ (x-\frac{2a\lambda^2}{\lambda^2-1})^2-(\frac{2a\lambda^2}{\lambda^2-1})^2+\frac{4a^2\lambda^2}{\lambda^2-1}+y^2=0$
$(x-\frac{2a\lambda^2}{\lambda^2-1})^2+y^2=(\frac{2a\lambda^2}{\lambda^2-1})^2-\frac{4a^2\lambda^2}{\lambda^2-1}$
$(x-\frac{2a\lambda^2}{\lambda^2-1})^2+y^2=\frac{4a^2\lambda^2}{(\lambda^2-1)^2}$
$(x-\frac{2a\lambda^2}{\lambda^2-1})^2+y^2=(\frac{2a\lambda}{\lambda^2-1})^2$
Hence the locus of P is a circle with centre $(\frac{2a\lambda^2}{\lambda^2-1},0)$ and radius $\frac{2a\lambda}{|\lambda^2-1|}$.
In fact, there is one value of $\lambda$, $\lambda=1$, where the locus isn't a circle - it is a straight line which is the bisector of AB, because in this case the distance from P to A is the same as the distance from P to B. Can you see where in the working above we needed the fact that $\lambda$ was not equal to 1, in order to get the equation of a circle?
For the second part of the question, Jordan noticed that since the tangent from the midpoint of AB to the circle will be perpendicular to the radius of the circle, the length of the tangent to this circle from the mid-point of AB can be calculated using Pythagoras:
In the case where $a=2$, $\lambda=3$, the radius of the circle is 3/2 and the distance between the midpoint of AB and the centre of the circle is 5/2 so by Pythagoras' theorem the length of the tangent is
$$\sqrt{(5/2)^2-(3/2)^2}=2$$
This is the same as half the distance between A and B, so the circle centred on the midpoint of AB with radius 2 will intersect the original circle in the tangential point. This is illustrated below:
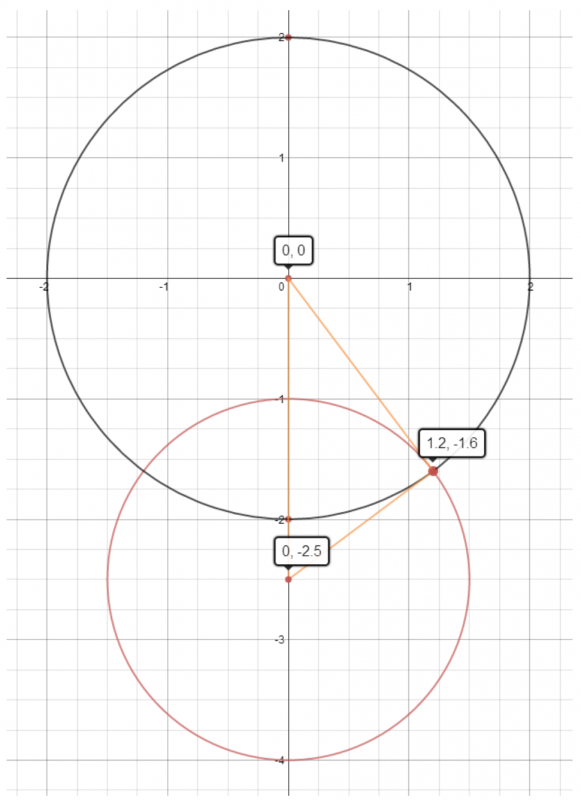
This distance turns out to be the same whatever the value of $\lambda$, so the tangential point always lies on the circle with centre the midpoint of AB and radius 2.
The shape traced by the tangential point for values of $\lambda <1$ is the half of the circle closest to A and for values of $\lambda>1$ is the half of the circle closest to B as illustrated below:
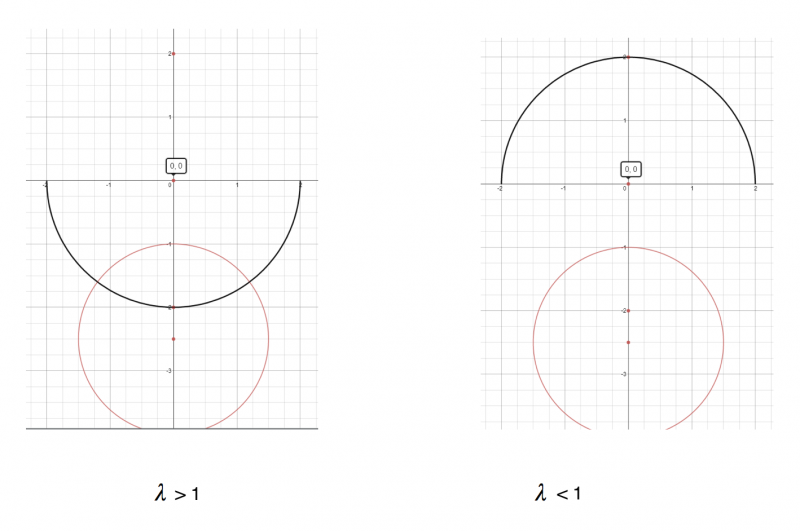
Elin has proved these observations in the general case where $a$ and $\lambda$ are not fixed:
Let M be the mid point of AB, C be the centre of the circle which is the locus of P, and T be the tangential point.
Then
$MC=\frac{2a\lambda^2}{\lambda^2-1}-a$
$CT=\frac{2a\lambda}{|\lambda^2-1|}$
Since MTC is a right angled triangle we can work out the length MT by Pythagoras:
$MT^2=MC^2-CT^2$
$=(\frac{2a\lambda^2-a(\lambda^2-1}{\lambda^2-1})^2-(\frac{2a\lambda}{|\lambda^2-1|})^2$
$=(\frac{a(\lambda^2+1)}{\lambda^2-1})^2-(\frac{2a\lambda}{|\lambda^2-1|})^2$
$=(\frac{(a(\lambda^2+1))^2-(2a\lambda)^2}{(\lambda^2-1)^2})$
$=(\frac{a^2(\lambda^4+2\lambda^2+1)-4a^2\lambda^2}{(\lambda^2-1)^2})$
$=(\frac{a^2(\lambda^4-2\lambda^2+1)}{(\lambda^2-1)^2})$
$=(\frac{a(\lambda^2-1)^2}{(\lambda^2-1)})^2$
$=a^2$
In conclusion $MT=a$, which in words says that the length of the tangent is $a$, whatever the value of $\lambda$ is, so the tangential point lies on a circle with centre the midpoint of AB, and radius $a$.
