Burning down
Problem

Two different candles are lit. They burn at different rates and one is 3 cm longer than the other.
The longer one was lit at 5.30 pm and the shorter one at 7 pm.
At 9.30 pm they were both the same length.
The longer one, burned out at 11.30 pm and the shorter one burned out at 11 pm.
How long was each candle originally?
Student Solutions
There are lots of nice solutions to this problem, using a range of different methods:
Rhiannon sent in this very nice solution.
It takes the big candle $6$ hours to burn down, and it takes the smaller candle $4$ hours.
At $9 \colon 30$, the big candle has $\frac{1}{3}$ of its time left to burn, so is $\frac{1}{3}$ of the original length. The small candle has $\frac{3}{8}$ of its time left to burn, so is $\frac{3}{8}$ of its original length.
Since the candles are at the same height at this time, $\frac{1}{3}$ of the large candle is the same height as $\frac{3}{8}$ of the small candle.
Writing $l$ for the height of the large candle and $s$ for the height of the small candle, we get:$$\frac{1}{3}l=\frac{3}{8}s$$Therefore $l=\frac{9}{8}s$.
This means the difference in heights is $l-s = \frac{1}{8}s$. But we already know the difference in heights is $3\text{cm}$, so $\frac{1}{8}s=3\text{cm}$, or $s=24\text{cm}$. Therefore the small candle is $24\text{cm}$ tall, and this makes the large candle $27 \text{cm}$ tall.
This solution uses fractions and proportional reasoning to determine the heights of the candles:

The next solution used a graphical method in order to find the height:
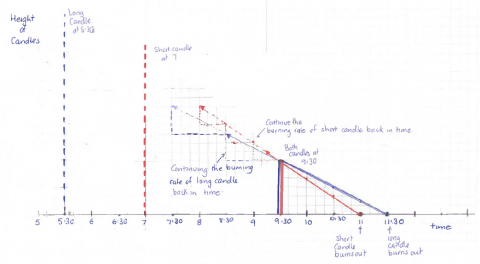
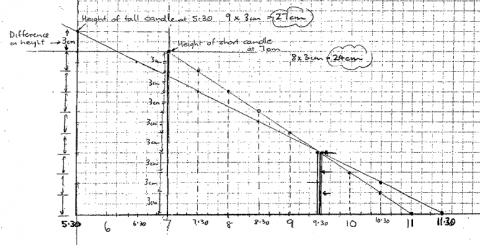
It is also possible to use algebra, as in the final solution below:
Let the height of the shorter candle be $x$ and the height of the taller candle be $x + 3$. Assume that the short candle burns down at $a$ cm per hour and the tall candle burns down at $b$ cm per hour.
The candles are the same length at 9.30 so:$$x-\tfrac{5}{2}a=x+3-4b$$Also the short candle burns out after 4 hours so:$$4a=x$$and the tall candle burns out after 6 hours so:$$6b=x+3$$Using these three equations gives:$$x-\frac{\tfrac{5}{2}x}{4}=x+3-\frac{4(x+3)}{6}$$which, when solved, gives $x = 24\text{cm}$.
Finally, originally the shorter candle was 24cm and the longer one was 27cm.
