Arrowhead
Problem
ABCD is a non-convex quadrilateral. The points P, Q, R and S are the midpoints of the edges of ABCD. You can change the shape of the quadrilateral ABCD.
What do you notice about the quadrilateral PQRS and its area as ABCD changes?
If you say that what you have noticed is always true, then you are making a conjecture. Can you prove your conjecture?
Student Solutions
Like Quad in Quad (June 1998) the key to this problem is using the fact that, when the midpoints of the sides of a triangle are joined, the join is parallel to the third side and half the length of the third side.
This solution came from Murat from Turkey.
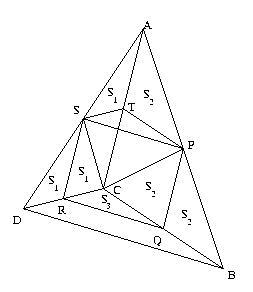
Due to the Thales relationship, SP and QR are both parallel to BD, thus to each other. Moreover they are half as long as BD. A similar relationship holds among PQ, RS and AC. Therefore PQRS is a parallelogram.
Let T be the midpoint of AC.
In the above figure, the areas of the triangles marked by the same symbol are obviously equal (look for triangles on equal bases which have the same height). Moreover Area (CST) = S 1 , Area (CPT)= S 2 and Area (TPS)= S 3 . The following equations are obviously true:
| Area (ABCD) = | 4( S 1 + S 2 ) |
| Area (PQRS) = | ( S 1 + S 2 + S 3 ) + ( S 1 + S 2 - S 3 ) |
| = |
2( S 1 + S 2 ) =
$\frac {1}{2}$ Area
(ABCD)
|