Area i'n it
Problem
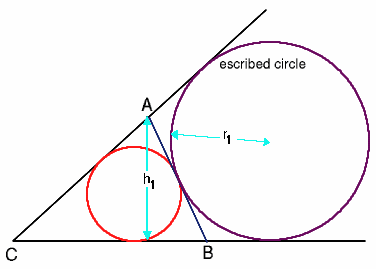
Triangle $ABC$ has altitudes $h_1$, $h_2$ and $h_3$.
The radius of the inscribed circle is $r$, while the radii of the escribed circles are $r_1$, $r_2$ and $r_3$ respectively.
Prove:
$\begin{equation} \frac{1}{r} = \frac{1}{h_1} + \frac{1}{h_2} + \frac{1}{h_3} = \frac{1}{r_1} + \frac{1}{r_2} + \frac{1}{r_3}. \end{equation}$
Student Solutions
Both Sue Liu, Madras College, St Andrews and Vassil Vassilev, Lawnswood High School, Leeds solved this one, well done!
Triangle $ABC$ has altitudes $h_1$, $h_2$ and $h_3$. The radius of the inscribed circle is $r$, while the radii of the escribed circles are $r_1$, $r_2$ and $r_3$. We prove that $${1\over r} = {1\over h_1} + {1\over h_2} + {1\over h_3} = {1\over r_1} + {1\over r_2} + {1\over r_3}.$$ Let $\Delta$ be the area of the triangle $ABC$ and let $X$ be the centre of the inscribed circle.
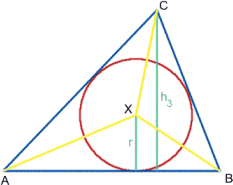
Clearly, $$\Delta = {\textstyle{1\over 2}}r.AB+ {\textstyle{1\over 2}}r.BC+ {\textstyle{1\over 2}}r.CA,$$ so that $${1\over r} = {AB + BC + CA\over 2\Delta}.$$ Also, $$\Delta = {\textstyle{1\over 2}}h_1.BC = {\textstyle{1\over 2}}h_2, \quad CA = {\textstyle{1\over 2}}h_3.AB,$$ thus $${1\over h_1} + {1\over h_2} + {1\over h_3} ={BC + CA + AB\over 2\Delta} = {1\over r}.$$ Now let $A'$, $B'$ and $C'$ be the centres of the escribed circles; see the diagram below. Also, for any triangle with vertices $U$, $V$ and $W,$ let $\Delta(U,V,W)$ denote its area.
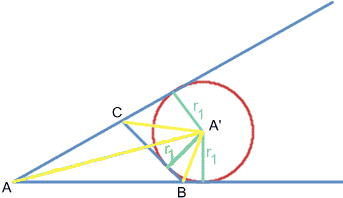
Considering the area of the kite $ABA'C$ by splitting it into two triangles in two different ways we get $$\Delta(A,B,C)+\Delta(B,A',C) = {\rm area}(ABA'C) = \Delta(A,B,A') + \Delta(A,C,A').$$ This gives (with $\Delta = \Delta(A,B,C))$ $$\Delta +{\textstyle{1\over 2}}r_1.BC = {\textstyle{1\over 2}}r_1.AB + {\textstyle{1\over 2}}r_1.CA,$$ and hence $${2\Delta\over r_1}= AB + CA - BC.$$ Similarly, $${2\Delta\over r_2}= AB + BC - CA, \quad {2\Delta\over r_3}= CA + BC - AB,$$ and adding these we get $$\eqalign{ 2\Delta\left({1\over r_1}+{1\over r_2}+{1\over r_C}\right) &= (AB + CA - BC) + (AB + BC - CA) + (CA + BC - AB) \cr &= (AB + BC + CA) \cr &= {2\Delta\over r}}$$ as required.
