Angle to chord
Weekly Problem 23 - 2008
A triangle has been drawn inside this circle. Can you find the length of the chord it forms?
A triangle has been drawn inside this circle. Can you find the length of the chord it forms?
Age
14 to 16
Challenge level
Problem
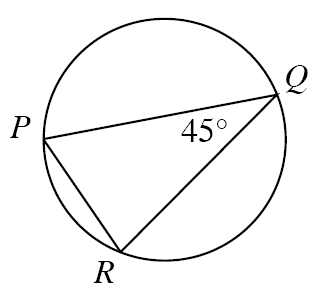
$P$, $Q$ and $R$ are points on the circumference of a circle of radius 4cm. $\angle PQR=45^o$. What is the length of chord $PR$?
Image
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Let $O$ be the centre of the circle.
Then $\angle POR=90^{\circ}$ as the angle subtended by an arc at the centre of a circle is twice the angle subtended by that arc at a point on the circumference of the circle.
So triangle $POR$ is an isosceles right-angled triangle with $PO=RO=4cm$. Let the length of $PR$ be $x$ cm.
Then, by Pythagoras' Theorem, $x^2=4^2+4^2=2 \times 4^2$ and so $x=4\sqrt{2}$.