Amicable Arrangements
Three of Santa's elves and their best friends are sitting down to a festive feast. Can you find the probability that each elf sits next to their bestie?
Problem
Three elves who work at Santa's factory are having a festive feast, and each one invites their best friend who works at the University of the North Pole. The three elves and their besties sit down at a round table. All of the possible seating arrangements of the six party-goers are equally likely.
(a) Show that the probability that each elf sits next to their bestie is $\frac 2 {15}$.
A good first step is to decide on some notation. Perhaps $E_1, E_2, E_3$ for the elves and $B_1, B_2, B_3$ for the associated best friends, so that $B_1$ is the best friend of $E_1$ etc.
This is a round table, so we can use symmetry to simplify the problem a bit. We can think of $E_1$ as being in a fixed seat, and then only have to worry about the positions of the other five party-goers. How many ways can you arrange five people?
You might find that diagrams (like the one below) are helpful.
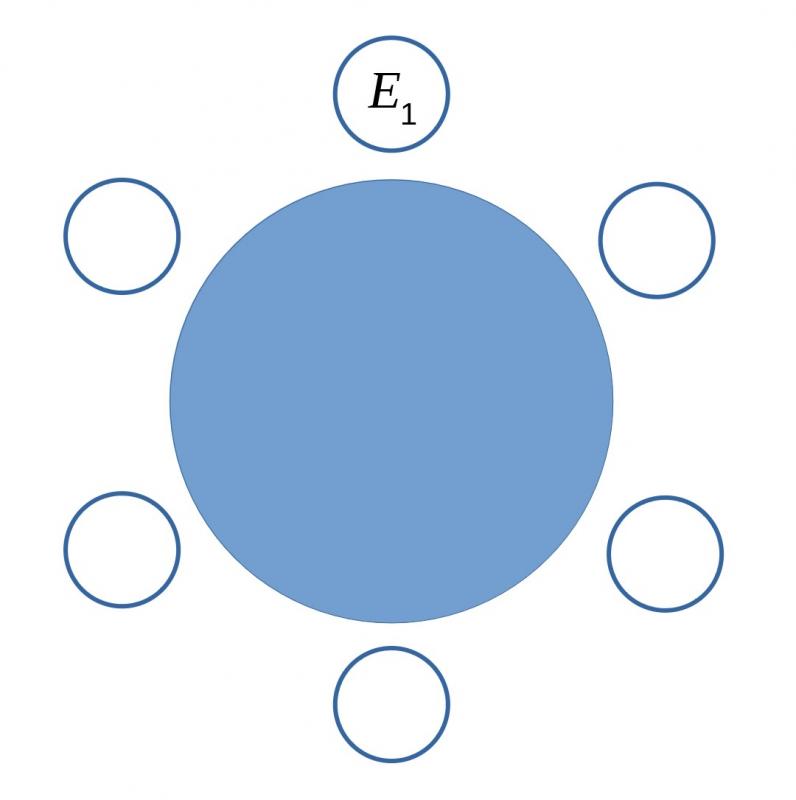
There are some more hints for this part in the Getting Started section.
(b) Find the probability that exactly two of Santa's elves sit next to their best friends.
You can start by considering the case when $E_1$ and $B_1$ are separated (and so $E_2$ and $B_2$ sit together, and $E_3$ and $B_3$ sit together).
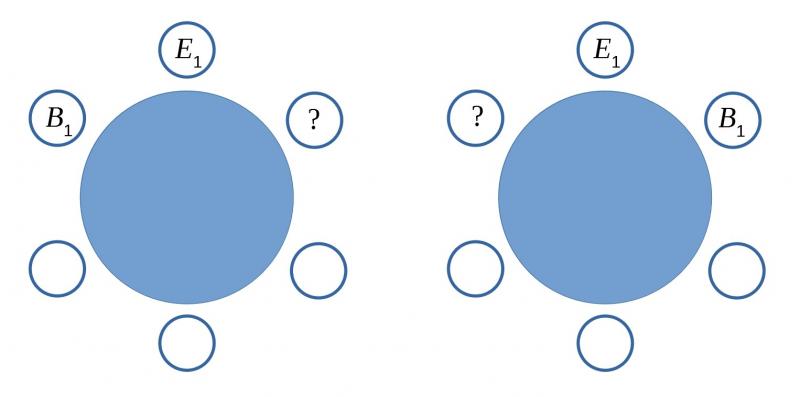
In the diagram below, which of the seats can $B_1$ not sit in if we are to have $E_1$ and $B_1$ separated? Are there any seats which mean that $E_1$ and $B_1$ are separated, but we cannot sit the other four elves in two pairs? How many seats can $B_1$ actually sit in?
How many options are there for the other seats? Maybe start with seat $1$?
Once you have found the number of ways of keeping $E_1$ and $B_1$ separated but the other two pairs are together, you can use symmetry to find the number of ways of keeping $E_2$ and $B_2$ or $E_3$ and $B_3$ separated.
(c) Find the probability that no elf sits next to their best friend.
Based on STEP Mathematics I, 2008, Q13. Question reproduced by kind permission of Cambridge Assessment Group Archives. The question remains Copyright University of Cambridge Local Examinations Syndicate ("UCLES"), All rights reserved.
Getting Started
Here are some further hints:
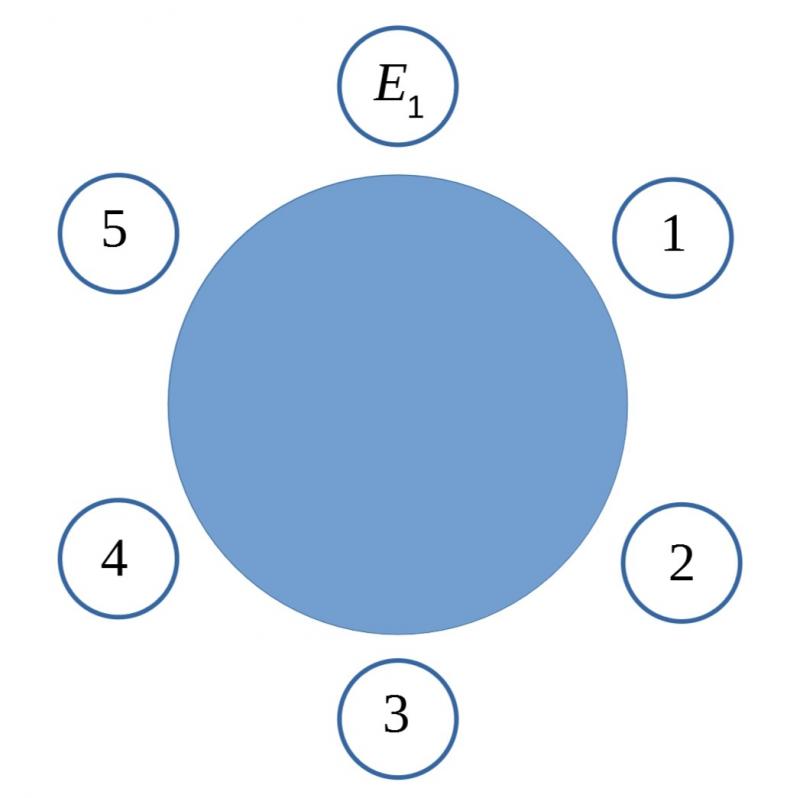
(a) Once $E_1$ is fixed you have a situation which looks like this:

How many ways can you seat the other $5$ people?
If we need to have every elf next to their best friend, in how many different seats can $B_1$ sit?
How many choices are there for the person sitting on the other side of $E_1$?
If the $5$ other people can sit anywhere with out restriction, then there are $5$ possible seats for $B_1$, 4 possible seats for $E_2$, 3 possible seats for $B_2$ etc. This means that there are $5 \times 4 \times 3 \times 2 \times 1 = 120$ possible arrangements.
$B_1$ can sit either to the right or the left of $E_1, as shown below:
It doesn't matter who sits on the other side of $E_1$, so there are 4 possibilities for the question mark in each of the two possible places for $B_1$.
How many choices are there now for the person sitting next to the second person placed next to $E_1$?
How many ways can you fill in the last two seats?
You should now be able to calculate the total number of ways in which everyone can be sat in such a way that each elf is next to their best friend. You also have the total number of ways in which everyone can be sat if there is no restriction. Can you now show that the probability that each elf sits next to their best friend is $\frac 2 {15}$?
Student Solutions
(a) Show that the probability that each elf sits with his bestie is $\frac2{15}.$
Anes, Jessica, Adil and Akua from London Academy of Excellence Tottenham, Isabella from King's College London Maths School, Sujay from Avanti House Secondary School, all in the UK, and Norman from Bangkok Patana School in Thailand seated the elves and besties one by one. This is Norman's work with Akua's diagrams:
There are 6 elves in total, E1, E2, E3, B1, B2, B3. If the elves are in a line (not a circle), isolating 1 elf from the list means that for example, E1 has an equal chance of sitting with either E2, E3, B1, B2, or B3. Allocating the best friend of the elf according to their number means that E1’s best friend is B1. If this is the case this means that there is a $\frac15$ chance that E1 sits with B1. [note that Norman assumes that B1 sits on our right hand side, and multiplies by 2 at the end]
If E1 is then sitting with B1, this means that E2, E3, B2, B3 are left.
There is a $\frac13$ chance that E2 will sit next to B2.
And now there is a $\frac11$ chance that E3 will sit next to E3.
Multiplying all the probabilities together will get $\frac1{15}$ that all the elves will sit next to their besties in a straight line. However, since they are sitting on a round table, the probability would double since everyone would now be sitting next to 2 others, therefore $\frac2{15}$ chance of sitting next to their bestie. [this corresponds to considering B1 on the other side of E1, and filling the table anticlockwise rather than clockwise. Akua accounted for this possibility by writing $\frac25$ rather than $\frac15$ for the first probability.]
Emily from Bishop's Wordsworth's Grammar School in the UK thought about all of the possible arrangements of elves and friends:

Nicole, and Adil from London Academy of Excellence Tottenham used a similar method, but pre-grouped each elf with their bestie. Here is Adil's work:

Nishad from Thomas Estley Community College in the UK had a similar method but expressed it in a different way (click to enlarge):

(b) Find the probability that exactly two of Santa's elves sit next to their best friends.
Emily, Isabella and Nishad considered all of the possible arrangements. Emily used diagrams and lists. Click to see Emily's work.

Isabella, Norman, Sujay and Jessica generalised for a neater approach this is Isabella's work (click to enlarge):
Nishad used words and logic. Click to see Nishad's work.


(c) Find the probability that none of Santa's elves sit next to their best friends.
Emily listed all the possibilities again. Click to see Emily's work.
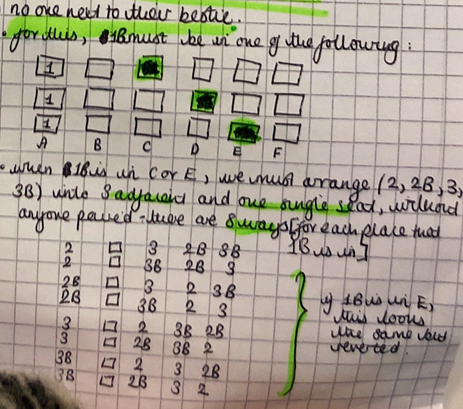
Sujay and Jessica considered the possible arrangements without drawing them all. This is Sujay's work:

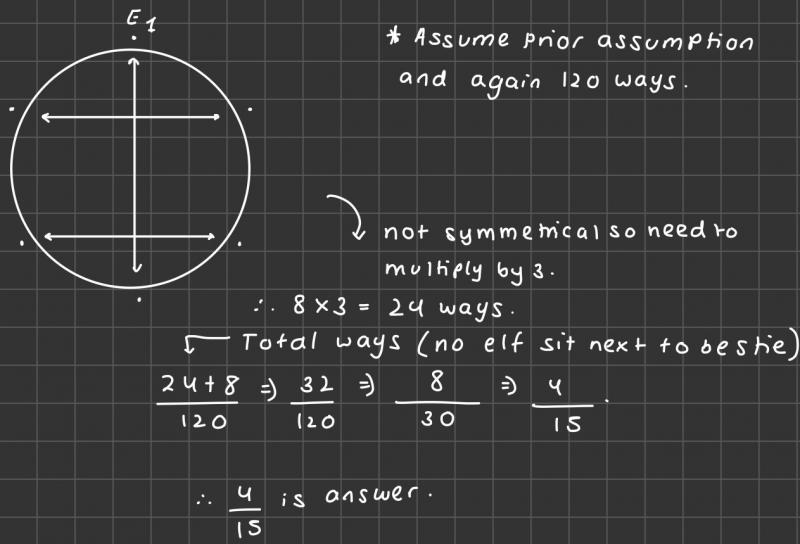
Isabella and Nishad used a process of elimination. This is Isabella's work:
Click to see Nishad's work.
Teachers' Resources
Why do this problem?
This problem is about arrangements and permutations, and also about logical thinking and systematic working, and presenting a solution clearly!
There are lots of hints and suggestions within the the problem to help students along (which reduce as they question progresses).
One of the key aspects which simplifies the problem is the symmetry of the situation. Since this is a round table, then we can consider the "top" of the table to be wherever Elf number 1 is. This means that we only need to consider what happens to the other 5 seats (and so we are only looking at $120$ possible arrangements rather than $720$).
Here you can find printable word and pdf versions of the problem.
Key questions
- What is special about a round table? How can we use the shape of the table to simplify the problem?
- How can we label the Elves and Besties to make things clearer and simpler?
- If we know where the first elf is, in which seats can his bestie sit so that they are sitting together? What if we want to keep them apart?
Possible extension
Students might like to try STEP Support Programme Foundation Assignment 6, which has some further questions on arrangements and probability.
Some similar STEP questions include 1995 STEP 1 Q12, 1997 STEP 1 Q1 and 2009 STEP 1 Q13. This can all be found via the STEP Database (you might like to type in "combinatorics" to find these quickly).

