Air routes
Find the distance of the shortest air route at an altitude of 6000
metres between London and Cape Town given the latitudes and
longitudes. A simple application of scalar products of vectors.
Problem
Image
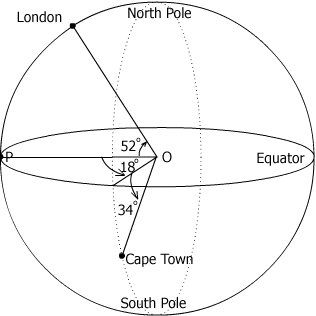
London is situated at longitude $0^o$, latitude $52^o$ North and Cape Town at longitude $18^o$ East, latitude $34^o$ South. Taking the earth to be a sphere with unit radius (and ultimately scaling by 6367 kilometres for the radius of the earth) work out coordinates for both places, then find the angle LOC where L represents London, O the centre of the earth and C Cape Town. Hence find the
distance on the surface of the earth between the two places. If a plane flies at an altitude of 6 kilometres and the journey takes 11 hours what is the average speed?
[You might also like to try the problems 'Over The Pole', which is a little simpler, and 'Flight Path' which is similar to 'Air Routes' but the method of solution given there is a bit different. ]
Getting Started
Find vectors $\overline{OL}$ and $\overline{OC}$ and use the scalar
product.
Student Solutions
The solution here uses scalar products of vectors. For a similar calculation using the cosine rule instead of scalar products see the problem Flight Path.
Good solutions were sent in by Thomas Lauffenberger, Angus Balkham of Bexhill College and Andrei Lazanu of School No. 205, Bucharest, Romania.
Here is Andrei's solution:
Two things are to be observed for solving this problem:
1) the angle $\alpha$ between two vectors ${\bf a}$ and ${\bf b}$ can be determined from their scalar product as follows: $$\cos \alpha = {{\bf a}.{\bf b}\over ab}$$ where a and b are the moduli of the vectors.
2) On Earth approximated with a sphere, if one knows the latitude and longitude of a point (city), the vectors with the origin in the centre of the Earth and ending in the respective city are completely determined.
The position on a sphere is usually described using the spherical coordinates: - the azimuthal angle, the angle in the xOy plane, and, the polar angle, from the z axis, as illustrated below:
Image
On the sphere $r$ is fixed, and I'll first work on the unit sphere. For the problem, the azimuthal angle gives the longitude, while the polar angle is ($90^o$ - latitude).
The relation between the spherical coordinates and the Cartesian ones on the unit sphere is: $$ x=\cos \theta \sin \phi,\ y = \sin \theta \sin \phi,\ z = \cos \phi.$$ For London, angle $\theta$ is ($90^o$ - $52^o$), i.e. $38^0$ and angle $\phi$ is 0 °. So, its coordinates are: $$x_1 = \sin 38^o \cos 0^o = \sin 38^o,\ y_1 = \sin 38^o \sin 0^o = 0,\ z_1 = \cos 38^o.$$ For Cape Town angle $\phi$ is $90^o + 34^o = 124^o$ and angle $\theta$ is $18^o$. Its coordinates are: $$x_2 = \sin 56^o \cos 18^o,\ y_2 = \sin 56^o \sin 18^o,\ z_2 = \cos 124^o = -\cos 56^o.$$
The scalar product of the two vectors characterised by their Cartesian coordinates: $\vec{OA}=x_1{\bf i}+y_1{\bf j} + z_1{\bf k}$ and $\vec{OB}=x_2{\bf i}+y_2{\bf j} + z_2{\bf k}$ is $$\vec{OA}\cdot \vec{OB}= x_1x_2+y_1y_2+z_1z_2.$$ The product of the vectors corresponding to London and Cape Town is: $$\vec{OL}\cdot \vec{OC}= \sin 38^o \sin 56^o \cos 18^o - \cos 38^o \cos 56^o = 0.0447754018.$$
So, if angle $LOC$ has its cosine value 0.0447754018, then its measure is $87.43370046^o$.
Each two points of a sphere are on a big circle of the sphere, having as centre the centre of the sphere. The angle between these points is the angle determined above.
The circumference of the Earth (considering it is a sphere) is: $2\pi \times 6367$ km
This value corresponds to $360^o$. So, to the angle $87.43370046^o$ corresponds the following distance in kilometres: $${87.43370046 \over 360} \times 2\pi \times 6367 = 9716.079$$ which we round to 9716 km.
I looked in Encarta and I found that the distance between the two cities is 9689 km, so the approximation is very good.
The distance traveled by the plane is a circular arc, with radius 6373 km. Applying a similar procedure, I observe that the plane traveled 9725.2359 km.
The formula for obtaining the speed is v = d/t, where d is the distance and t - the time. So, the average speed is 884 km/h (to 3 significant figures), a value that is again reasonable.
Teachers' Resources
The question asks for the use of 3D coordinates and scalar products
in a very practical context.
