Agile algebra

1.  $(x + 3)^4 + (x + 5) ^4 = 34$

Nayanika from the Tiffin Girls' School in the UK solved this equation neatly, using a substitution. There is one small error which is corrected.

Image

The solution is $x=-4\pm\sqrt2.$

2.  $(x-1)(x-3)(x-5)(x-7)+15=0$

Nayanika used another substitution:

Image

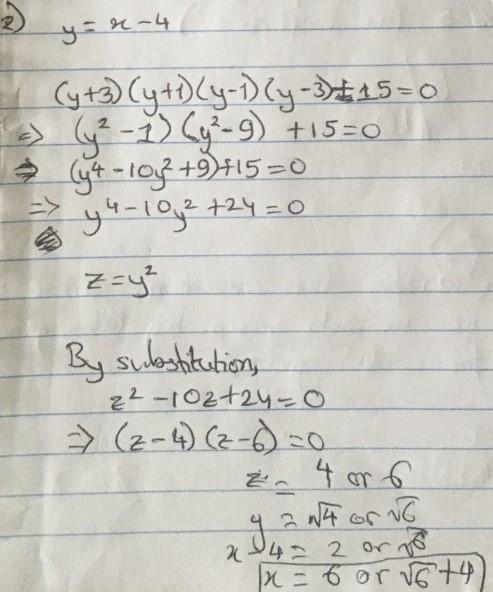
Remember that $y=-2,-\sqrt6$ are also solutions, which give $x=2, 4-\sqrt6$

3.  $(x-4)(x-5)(x-6)(x-7)=1680$

Patrick from Woodbridge shool sent in this solution:      

 

Let us rewrite the equation with $a = x-7$, then we have $(a+3)(a+2)(a+1)a = 1680.$

Note that $a(a+3) = a^2 + 3a$, and $(a+2)(a+1) = a^2 + 3a + 2$, so $(a+2)(a+1)(a+3)a = (a^2 + 3a)(a^2 + 3a + 2).$  Let us then take $y = a^2 + 3a$, then $y(y+2) = 1680$ and $y^2 + 2y - 1680 = 0.$

Factorising, we find $(y-40)(y+42) = 0$, so $y = -42$ or $+40$. Since $y = a^2 + 3a$, then we have either: $40 = a^2 + 3a$, so $(a+8)(a-5) = 0$ and $a = -8$ or $5$.

Alternatively $-42 = a^2 + 3a$, which has no real roots. Therefore, we have $a = -8$ or $5$. Then, since $a = x - 7$, $x = a + 7$, so $x = -1$ or $12$.

We will test this by substitution: $(-1-4)(-1-5)(-1-6)(-1-7)$, so for each bracket (-a-b) we can take out the negative to give -(a+b). There are four such brackets, so there are four -1 factors removed, which multiply to give 1. Therefore, $(1+4)(1+5)(1+6)(1+7) = 5\times 6\times 7\times 8 = 1680.$ Similarly, $x=12$ gives us $8\times 7\times 6\times 5 = 1680.$

 

Well done Patrick. An alternative substitution could be $t= x - 5\frac{1}{2}.$

Tom from The Skinners School used a substitution for the equation $x^4-8x^3 + 17x^2-8x+1=0,$ but it is not the one we suggested. Here is Tom's solution:

$f(x) = x^4 - 8x^3 + 17x^2 - 8x + 1 = 0$

use substitution $z = x^2 - 8x + 1$

so $f(x) = zx^2 + 15x^2 +z = 0$

use same substitution again for the $x^2$ term that is multiplied with $z$

$f(x) = z(z^2 + 8x - 1) + 15x^2 + z = 0$ 

$= z^2 + 8xz - z + 15x^2  + z$

$= z^2 + 8xz + 15x^2$

$= (z+3x)(z+5x)$

so $x^2 - 5x + 1 = 0$

and $x^2 - 3x +1 =0$

you can solve these quadratics using the quadratic equation and this gives you the four solutions to $f(x) = 0.$

Could the substitution we suggested, $z = x + \frac1x$ help with the next two equations?

4.  $x^4-2x^3 -6x^2-2x+1=0$

5.  $x^4-2x^3+2x^2-2x+1=0$

Tom also sent in a solution to the extension, $(8x+7)^2(4x+3)(x+1)=\frac{9}{2}$

let $y = x+1$

$(8y-1)^2(4y-1)(y) = \frac{9}{2}$

$(64y^2-16y+1)(4y^2-y) =\frac{9}{2}$

let $z = 4y^2 - y$

$(16z+1)(z) = \frac{9}{2}$

$16z^2 + z =\frac{9}{2}$

$32z^2 + 2z - 9 = 0$

$(2z-1)(16z+9) = 0$

Second bracket gives no real values of $y$ so for real solutions, $2z - 1 =0$

$z = \frac{1}{2}$

$4y^2 - y = \frac{1}{2}$

$8y^2 -2y -1=0$

$(4y+1)(2y-1)=0$

$y= -\frac{1}{4} \text{and} \frac{1}{2}$

$x = -\frac{5}{4} \text{and} -\frac{1}{2}$