1, 2, 3, 4, 5
2 out of 3
Using the numbers 1, 2, 3, 4 and 5 once and only once, and the operations x and รท once and only once, what is the smallest whole number you can make?
Problem
Using the numbers $1, 2, 3, 4$ and $5$ once and only once, and the operations $\times$ and $ \div$ once and only once, what is the smallest whole number you can make?
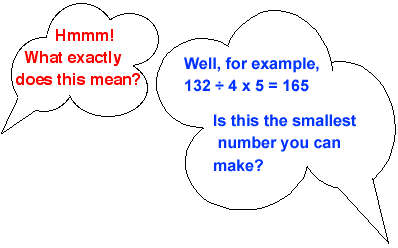
Getting Started
A calculator might help.
Student Solutions
Bethany from Tattingstone, Douglas from Burgoyne Middle School and Amelia who goes to Norland Place School all decided the answer to this problem was the number 1. Douglas said:
First I worked out which things seemed to make a good choice to start looking at. Multiplying by 1 seemed to be a good idea, although I found that this didn't make any whole numbers so I scrapped it.
Then I tried multiplying by two. The best answer I found was three (51/34x2).
Finally I tried multiplying by four. I found the best answer, it was one (13/52x4).
I didn't try five because I knew it wouldn't make less than one.This means the answer is 13/52x4.
Amelia told us:
Think of a big number to divide by. Try something ending in 4 as it will be divisible by 2.
After lots of experimenting I came up with 51x2/34=3.
I also came up with 52/13x4 but my teacher explained that this would only equal 1 if I could put brackets
around (13x4) or else it would be actually equal to 16.
Bethany used a calculator to move the numbers around and try different combinations. She arrived at 13x4/52.
Fantastic! Three different solutions to admire.
Teachers' Resources
Using NRICH Tasks Richly describes ways in which teachers and learners can work with NRICH tasks in the classroom.
Why do this problem?
This short problem could be used to start a lesson or fill a gap made by those who finish early. It will promote thinking about numbers and offers opportunities to practise multiplication and division.
Key questions
Possible extension
Learners could make the largest number that they can using the same rules, and then as many results in between as possible.
Possible support
Using a calculator will help some children.