Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Painted Cube



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We received many correct solutions to this problem - from Adam from Knoxdale P. S., Ramsudheer from Smith Elementary School, Ojaswi, Bill from King's St. Alban's, Chantell, Billy, Connor and Chanel from Arunside, Rajeev from Fair Field Junior School, Jessica from Beeston Rylands Junior School, Finlay from Gledhow Primary School, Olivia and Martha from St.Johns C.E. Primary School, Yuki from King's School Ely, Belky, Mark from Gledhow Primary School, James and Arjun from Wilson's, William from Barnton Community Primary School Alice, Joanna from Woodmill High School, Derek, Robert from Ardingly College Junior School, Joe from Lady Manners School in Bakewell and students from Rawdon Littlemoor Primary School. Well done to you all.
Alan wrote:
Chantell, Billy, Connor and Chanel sent us this clear table summarising their findings. Rajeev sent us a very similar table of results.
Yuki noticed that:
Students from Crestwood College also mentioned this.
Arjun also worked on this:
Mark from Gledhow Primary School produced this spreadsheet.
Robert summarised his findings as follows:
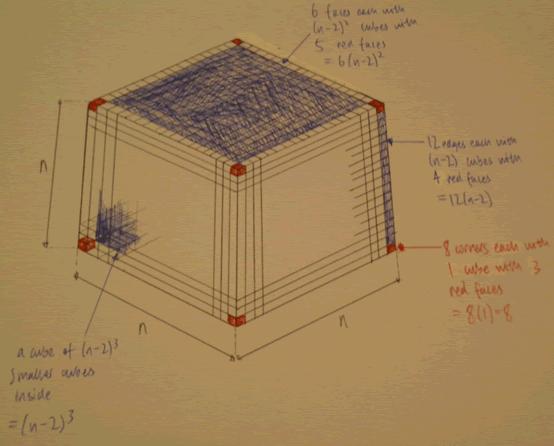
"Let n= number to be cubed
No. of small cubes with 6 red faces = (n-2)$^3$
This is because the cubes in the centre remain clean, so you must take one off either edge and then cube it.
No. of small cubes with 5 red faces = 6(n-2)$^2$
This is because there are 6 faces to the cube, and only the ones not on the edge remain clean on 5 sides. So you must take one off either edge, then square it, then multiply it by the 6 faces.
No. of small cubes with 4 red faces = 12(n-2)
This is because there are 12 non-corner edges which is multiplied by n (which = 1 whole edge) -2 for the 2 corners.
No. of small cubes with 3 red faces = 8
This is because there are always 8 corners
The total No. of small cubes is always n cubed"
Alice described her findings in a similar way:
"First of all I imagined a 3x3x3 cube being dipped in paint - that's how I worked the first one out then we worked out that
1) the number of cubes with 6 red faces equalled (n-2)$^3$, like when you take the skin off a square orange, taking a layer off each side
2) 5 red faces 6(n-2)$^2$, which is like the above but for the faces instead of the middle (it's squared not cubed ) and you have to multiply it by 6 because there are 6 faces
3) 4 red faces 12(n-2) this is the edges, take 2 for the corners and multiply it by 12 because that's how many edges there are
4) 3 red faces always got to be eight because these are corners (unless your cube is 1x1x1)
5) total number of small cubes is n$^3$
Joe, Derek and Alice completed the table of results:
|
Size of large cube |
No. of small cubes with 6 red faces |
No. of small cubes with 5 red faces |
No. of small cubes with 4 red faces |
No. of small cubes with 3 red faces |
Total No. of small cubes |
|
3 x 3 x 3 |
1 |
6 |
12 |
8 |
27 |
|
4 x 4 x 4 |
8 |
24 |
24 |
8 |
64 |
|
5 x 5 x 5 |
27 |
54 |
36 |
8 |
125 |
|
6 x 6 x 6 |
64 |
96 |
48 |
8 |
216 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 x 10 x 10 |
512 |
384 |
96 |
8 |
1000 |
|
23 x 23 x 23 |
9261 |
2646 |
252 |
8 |
12167 |
|
n by n by n |
(n-2)$^3$ |
6(n-2)$^2$ |
12(n-2) |
8 |
n$^3$ |
NB. The values for n are correct unless n = 1.
When n = 1 the single cube will have no red faces.
In her conclusion Alice added that in the second column the numbers were all cubic numbers, in the third column square numbers times 6 and in the fourth column multiples of 12.
Belky explained how she reached her results. This is how she arrived at a formula for the number of cubes with two faces painted :
Both William and Derek showed that:
We can verify that all cubes have been accounted as:$$(n-2)^3 + 6(n-2)^2 + 12(n-2) + 8 $$ $$= (n-2) (n^2 - 4n + 4) + 6 (n^2 - 4n + 4) + 12n - 24 + 8 $$ $$ = n^3 - 4n^2 + 4n - 2n^2 + 8n -8 + 6n^2 - 24n + 24 + 12n - 24 + 8 $$ $$ = n^3 $$
Derek added this diagram to support his conclusions:
Mollie and Hannah from Comberton Village College also sent in some excellent solutions; follow the links below to see their work:
Mollie's solution
Hannah's solution

