Digit discovery
Here is an interesting property about two sets of digits. Can you work out what the digits might be?
Problem

There are two digit cards in front of Rafe, and two in front of Jasmine. Each card shows a digit from 0 to 9.
Rafe says:
| "I've just noticed something interesting. If you add together the two numbers in front of me, the answer is the same as what you get when you multiply the two numbers in front of you." |
What might the digit cards be?
Are there any other possible answers?
Then, Jasmine says:
| "I've noticed something else - it works the other way round as well. The sum of my numbers is the same as the product of your numbers." |
What might the digit cards be now?
Can you find all the possible answers? How will you know when you've found all of them?
Extension
Rafe and Jasmine take two new digit cards each.
Rafe says:
| "There's something interesting about these cards as well. If you subtract one of my numbers from the other one, the answer is the same as what you get when you divide one of your numbers by the other one." |
Jasmine says:
| "And it still works the other way round! Subtracting my numbers gives the same answer as dividing your numbers." |
What might the digit cards be?
Are there any other possible answers?
Can you find all the possible answers? How will you know when you've found all of them?
Getting Started
What might the sum of two numbers between 0 and 9 be? How can that help you narrow down the possibilities?
It might also be helpful to think about this question: when you multiply two numbers together, is the product bigger or smaller than the sum of those two numbers? Does the answer to that question depend on what the two numbers are?
Student Solutions
Well done to everybody who had a go at this activity. We received a lot of solutions from children who found digit cards that would work for Rafe's statements but not for Jasmine's. In this solutions page, we'll be focusing on the solutions which considered both statements.
Hugo, Kwontay and Rory from Wharncliffe Side Primary School in England found that if all the cards showed the digit 2 then both statements would work:
2+2=4 2×2=4 and the other way round can be 2×2=4 and 2+2=4
Nethya from Brentwood School in England and Poppy from CHPS in Australia found the same solution. Poppy explained:
While there are other possible numbers for this problem, I chose Rafe's to be 2 and 2. This means Jasmine's have to multiply to 4. Possible digits are either 1 and 4 or 2 and 2, like Rafe.
However the answer has to be 2 and 2 because of what Jasmine says about the product and the sum. If Jasmine and Rafe both have 2 cards that means if they multiply or add them the answer will always be 4, concluding both problems.
Saul, Erin and Liora from Eden Primary in England also found the solution where all the digits were 2, and they found another solution as well. Saul explained their method:
I found two solutions for the problem 'Digit discovery', the answers (that I found) being 0,0,0 and 0 and 2,2,2 and 2.
I started working out the answer by just guessing random numbers. Quickly, I realised this was not a good way to work it out, and so I decided to change the method. My new method was to start on 0 and go up, seeing if I could find any solutions for each number.
After starting this new method, I immediately realised I could do 0,0,0 and 0 and then when I climbed up the numbers, I found that 2,2,2, and 2 could be an answer.
I stopped then, yet I am sure if I had carried on, I would have found many more answers.
You're right, Saul - there is at least one more possible answer!
Some children looked at the case where repeated digits were not allowed. Daniel, Syan, Elliot, Rory, Jasper, Rohan, Kosara, Naomi, Darcie, Arushi and Niam from Banstead Prep School in England and Charlie from Parkside Primary School in Australia found a different solution which satisfied this extra condition.
Niam drew a table and looked for repeated calculations in the 'Jasmine' and 'Rafe' column to find pairs of numbers that worked both ways round. The picture below can be clicked on to enlarge it:
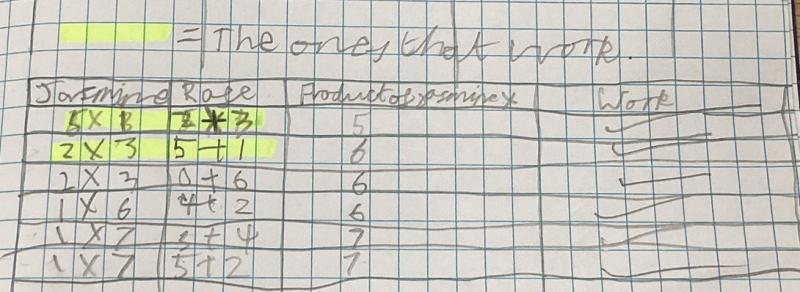
Niam explained how to restrict the possibilities by considering the highest the answer can be:
If you draw a table you can figure out the only possible answer because the highest you can add up to is 16. (Niam is not allowing repeated digits such as 9+9.)
Rory, Jasper and Rohan thought that a sum of digits of 11 or higher would be too big, but they didn't explain how they knew. I wonder if it has something to do with what happens if you multiply two digits with a sum of 11 or higher?
Tejas, Valerie, Varun, Kaumudi, Dhwani, Ira, Prathamesh, Adhrit, Delissaa and Riyansh from Ganit Kreeda in Vichar Vatika, India also found the solution where one pair of numbers is 2 and 3 and the other is 1 and 5. Adhrit drew a table to find all the possible ways of pairing up the cards so that the sum of Rafe's cards is the product of Jasmine's:
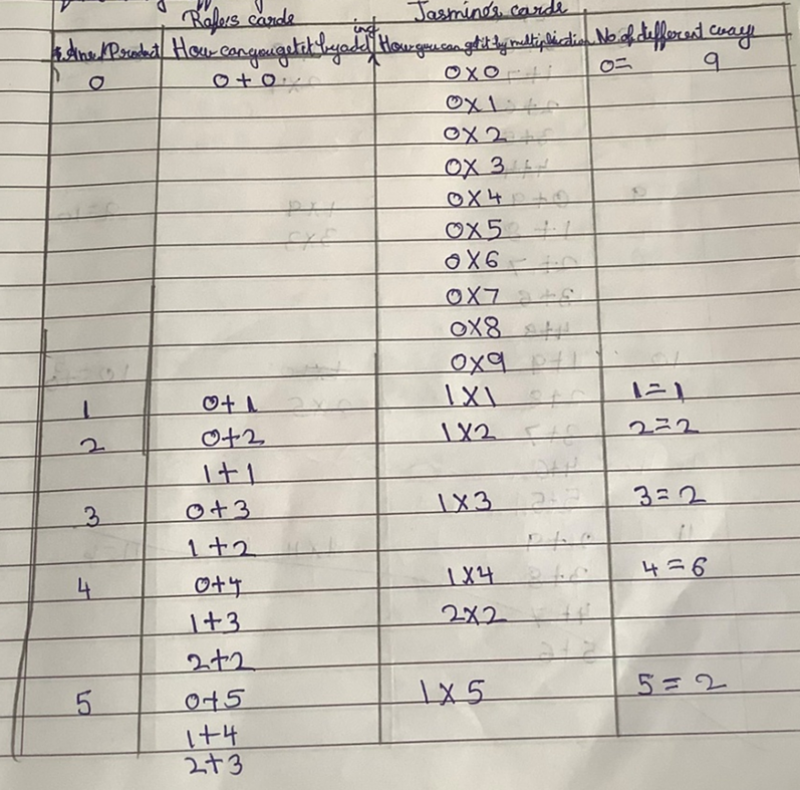
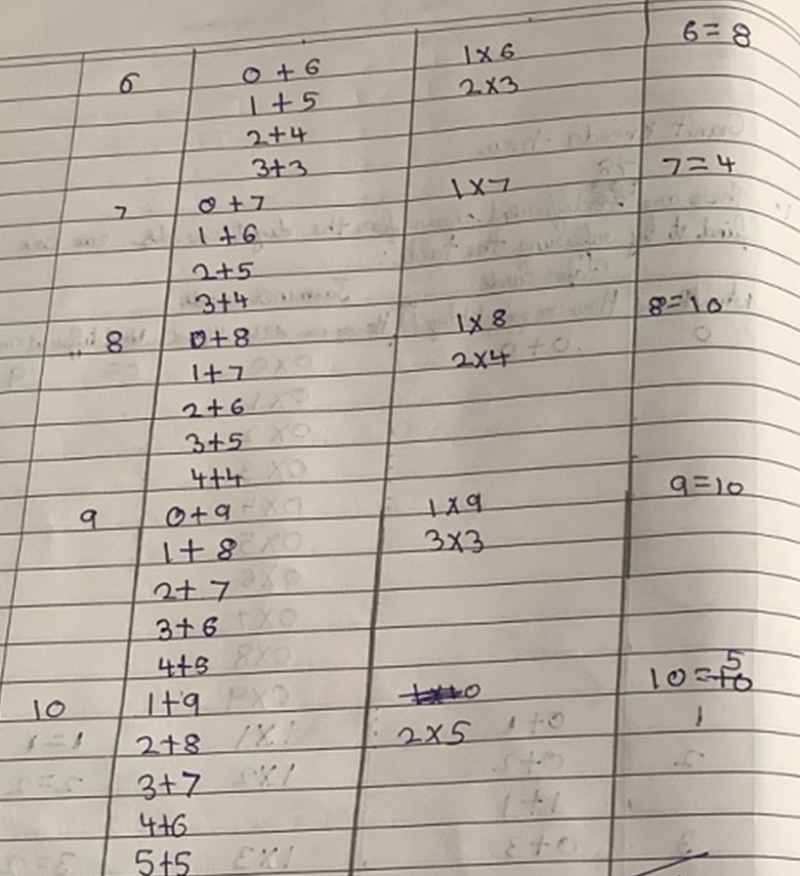
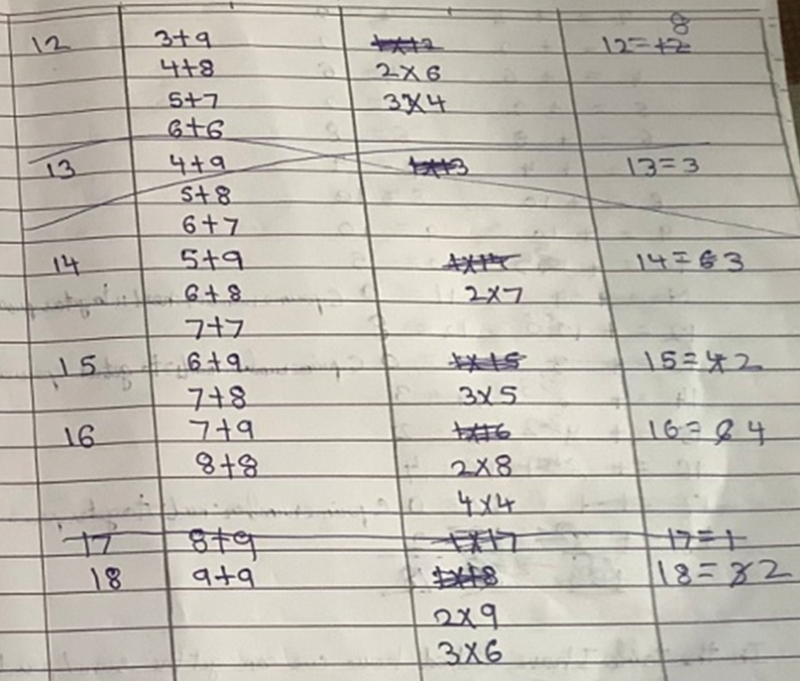
Adhrit explained:
In the table I have listed how we can get the sum/product of the numbers. Then I listed out the ways by which we can get it by adding and after that I did the same with multiplication.
| Rafe has: | Jasmine has: |
1, 5 1+5=6 1×5=5 | 2, 3 2×3=6 2+3=5 |
2, 2 2+2=4 2×2=4 | 2, 2 2×2=4 2+2=4 |
2, 3 2+3=5 2×3=6 | 1, 5 1×5=5 1+5=6 |
I know that I have found all possible answers because of the following:
I paired 1 with numbers from 1 to 9, then I paired 2 with numbers from 2 to 9 as 2 was paired with one in the starting I didn't pair 2 with 1 again and checked if they work out.
I continued the pairing method till 4 paired from 4 to 9.
Then I stopped with 4 and did not do 5 because 5 will be paired with 5 in the start and their product will result in 25. We cannot get 25 as a sum of numbers from 0 to 9 as 9+9=18.
Then I found that these were the only answers.
Adhrit hasn't included the solution where all digits are 0 in this table, but I think together we have found all the possible solutions for the first part of the task: the solution where all digits are 0, the solution where all digits are 2, and the 1, 5, 2, 3 solution.
Some children thought about possible solutions for the extension question. Elliot from Banstead Prep School, Sishan, Mia, Toby and William found this solution:
The cards that Jasmine has for the extension are 4 and 2 and the cards that Rafe has are 4 and 2.
Daniel from Brentwood School in England described a method for finding solutions to the extension question:
Since the division of two single-digit numbers (except for dividing by 1) rarely results in a whole number within the range of single-digit subtractions, the solutions are likely to involve numbers that are close to each other or involve 1 as one of the divisors.
Rory, Jasper and Rohan from Banstead Prep School in England and Yuto S from St. Mary's International School in Tokyo, Japan found that one pair of numbers could be 1 and 4 and the other could be 2 and 6. Yuto S showed why this works:
4 - 1 = 6 ÷ 2
6 - 2 = 4 ÷ 1
Lots of children seemed confident that they had found all possible solutions for the extension question, but there is at least one more way of doing this. Please email us to let us know if you think you've found any solutions that aren't featured here.
Thank you as well to the following children, who also sent in similar solutions: Jamie; Avyu, Constantine, Ishan, Cooper, Zain, Deen, Sam, Jaelyn, Arthur and Logan from Banstead Prep School in England; Monty, Ellis, Eli, Evie, Kamila, K and E from CHPS in Australia; and Hadia and Zidan from Pristine Private School in Dubai, UAE.
Teachers' Resources
Why do this problem?
This problem provides an engaging context in which learners can explore whether the sum or the product of two numbers is larger, and how this depends on the numbers in question.
Possible approach
Begin by introducing just the first part of the task - what could the two pairs of numbers be, if one pair of numbers multiplies together to give the sum of the other pair of numbers? Allow some time for pupils to work on this.
Before the next part, it may be beneficial to go over the definitions of the words 'sum' and 'product' as a whole class. Introduce the second part of the task and make sure that everybody understands what is being said - when you multiply Rafe's two numbers together, you get the sum of Jasmine's numbers, and vice versa. You might like to give some examples with numbers, but make sure not to give away any solutions!
Provide some time for pupils to work in pairs on this activity. Make it clear that there are two goals of the activity: to find some solutions that satisfy all the conditions, and to be sure that all possible solutions have been found. (Some children might find the solutions very quickly, and will then be focusing on ruling out other possibilities or reasoning about which solutions can't possibly work.)
Let the children decide how to record their working. You might like to make digit cards available for learners to move around, but duplicate numbers will need to be provided as there's no guarantee that the solution won't involve the same digit multiple times.
After a while, stop the class and share some different ways of working that different pupils have been using. Try to avoid sharing any solutions that have been found (although children will naturally want to share these with each other!) but instead focus on ways of working systematically to check all the possibilities. Are there any ways of narrowing down which pairs of digits to check? Could one pair of digits be 9 and 9, given that the product of these numbers would be 81? Children may have noticed that some pairs of numbers have a sum that can't be factorised using the digits 0-9 - is there any pattern to which pairs of numbers these are?
At the end of the session, bring the class back together and ask pupils to share how they got on with the activity. How can we be sure that there aren't any more solutions?
You might like to spend another session on the extension activity, or you could introduce it as a 'simmering' activity (where pupils could think about it over the course of a week or so, and add their thoughts to a working wall of ideas).
Key questions
What is the sum of those numbers? What is the product?
Is there a different pair of numbers that add up to the product of the first pair? What would the product of that second pair be?
Is the product of two numbers generally bigger or smaller than the sum of the same two numbers? Does this depend on the numbers you're using?
How do we know we don't need to check that pair of numbers? What is it about their sum/product that means it won't be possible to find a solution that includes them?
Possible support
Some children will benefit from having digit cards to move around, and it might be helpful to have times tables grids available so that learners don't get stuck at the multiplication stage of the task.
Possible extension
Children might like to consider what would happen if the cards were allowed to contain numbers of any size rather than just numbers from 0 to 9. Are there any more solutions in that case? (There is an interesting solution when negative numbers are allowed!)
Learners could also focus on coming up with a convincing argument for why there aren't any other possible solutions. They might like to write up their ideas or create a poster going through some of the different things they've learnt in the process of working on this activity, explaining why they think they've found all the possible solutions.
The extension at the bottom of the problem page could also be used as a follow-on for the main activity.
