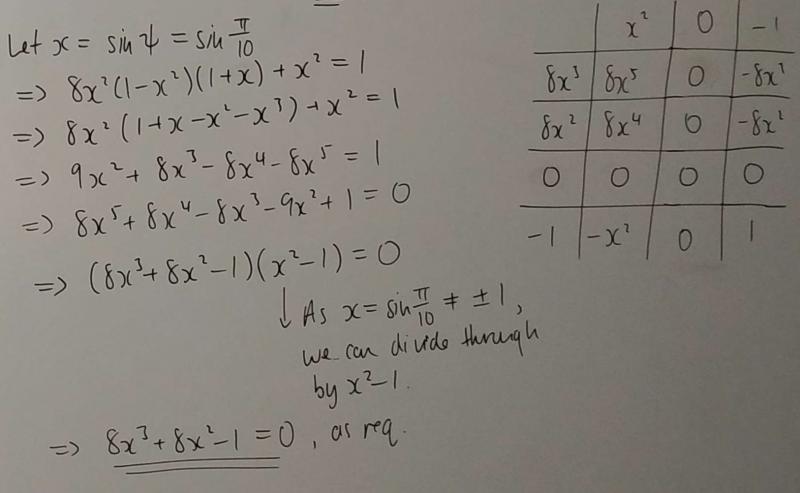Tri-angled trig
Problem
If $\theta+\phi+\psi=\tfrac{1}{2}\pi,$ show that $$ \sin^{2}\theta+\sin^{2}\phi+\sin^{2}\psi+2\sin\theta\sin\phi\sin\psi=1. $$
Below are some hints about how you might approach this part of the question.
Can you express $\cos \left(\frac{\pi} 2 - \alpha \right)$ in another way? It might help to sketch $\cos x$ and $\sin x$ in the range $0 \le x \le \frac{\pi} 2$. Can you apply this when $\alpha = \psi$?
What is the value of $\sin(\theta+ \phi + \psi)$?
There is more than one way to solve this problem, so you might not find all of the above helpful for your method, and you might need other identities as well!
By taking $\theta=\phi=\tfrac{1}{5}\pi$ in this equation, or otherwise, show that $\sin\tfrac{1}{10}\pi$ satisfies the equation $$ 8x^{3}+8x^{2}-1=0. $$ Again, here are some hints.
The algebra is slightly easier if you start by using $[\sin 2 \psi]^2=[2 \sin \psi \cos \psi]^2 $.
You will probably end up with a quintic (polynomial of degree 5). This can be factorised so that one of the brackets is equal to the required cubic. You can use long division of polynomials if you want, but "inspection" is quicker and less error prone here!
Based on STEP Mathematics I, 1991, Q1. Question reproduced by kind permission of Cambridge Assessment Group Archives. The question remains Copyright University of Cambridge Local Examinations Syndicate ("UCLES"), All rights reserved.
Student Solutions
Show that $\sin\theta+\sin\phi+\sin\psi=1$
Leo from Stowe School, Edward from Sir William Robertson Academy and James from St Bernards all began from $\sin{(\theta+\phi+\psi)}=1.$ This is James's work (click on the image to open a larger version):
Joshua from Bohunt Sixth Form and Dylan from Brooke Weston used the substitution $\psi=\frac\pi2-\theta-\phi.$ This is Dylan's work (click on the image to open a larger version):
Dibyadeep from Greenhill School in the USA split the sines up in a different way, and wrote up the results in the format of a paper. Click here to download Dibyadeep's paper, which also includes the second part of the problem.
Show that $\sin{\frac\pi{10}}$ satisfies the equation $8x^3+8x^2-1=0$
Leo, Joshua, Dylan, James and Edward all solved the second part of the problem by substituting $\sin\frac\pi{10}$ as $x$ (or $s$), expanding and factorising. Leo and Dylan factorised by inspection. Here is Leo's work:
Dylan was a bit more explicit about the facotrising. Click to see some of Dylan's work.
Joshua, James and Edward used the factor theorem, and Edward used polynomial long division to factorise the quintic. Here is some of Edward's work:
Dibyadeep didn't need to factorise at all, because at this point in Dibyadeep's working, $1-x^2$ was written as $\cos^2\frac\pi{10}.$ Click here to download Dibyadeep's paper.
Teachers' Resources
Why do this problem?
This problem requires students to keep track of an extended algebraic argument, and provides the opportunity to talk about layout of solutions (such as "one equal sign per line, all equal signs aligned").
Students will need to be resilient as the solution method is not entirely clear, and the problem required quite a lot of trigonometric manipulation in order to solve it.
Key questions
- What do we know?
- What is special about $\dfrac{\pi} 2$?
- Which trig relationships might be helpful?
- Can you relate $\sin(\theta + \phi)$ to a trig function involving $\psi$?