Quadrilaterals in a hexagon
Problem
This regular hexagon has been divided into 36 triangles. Can you convince yourself that all the triangles are congruent?
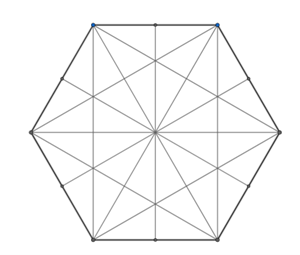
Here is a printable sheet with copies of the hexagon to draw on
By shading in some of the triangles, which of these shapes can you make?
- Kite
- Rectangle (that is not also a square)
- Square
- Parallelogram (that is not also a rectangle, square or rhombus)
- Rhombus (that is not also a square)
- Trapezium (that is not also a parallelogram)
- Delta/Arrowhead
You should have found that only one of those shapes is not possible.
Can you fit one of each different classification of quadrilateral on the same hexagon with no overlaps?
OR
By shading in some of the triangles, which of these shapes can you make?
- Kite
- Rectangle
- Square
- Parallelogram
- Rhombus
- Trapezium
- Delta/Arrowhead
You should have found that only one of those shapes is not possible.
Can you fit one of each different classification of quadrilateral on the same hexagon with no overlaps?
Note for this activity: Some of these shapes are special kinds of other shapes - for example, a square is a specific type of rectangle, and a rectangle is a specific type of parallelogram. For this activity, each quadrilateral you draw can only represent its most specific classification: it it's a square, you can't use it as a rectangle, and if it's a rectangle, you can't use it as a parallelogram.
Thank you to Glyn Philip Richards who submitted this problem to NRICH.
