How Shady?
What fraction of this triangle is shaded?
Problem
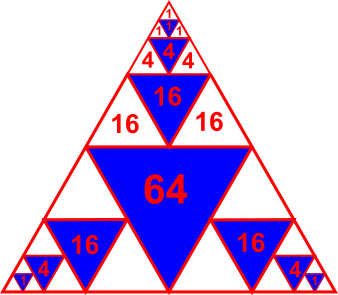
The diagram below shows an equilateral triangle with some triangles shaded inside it.
Each shaded triangle is equilateral and touches the sides of the largest triangle and of the shaded triangles next to it.
What fraction of the whole triangle is shaded?

This problem is taken from the World Mathematics Championships
Student Solutions
Answer: $\dfrac{127}{256}$
Largest shaded triangle: $\dfrac14$ of the whole triangle

Next largest shaded triangle: occupies $\dfrac14$ of $\frac14$ $\therefore$ area $=\frac1{16}$

That means the shaded triangles of this size occupy $3\times\dfrac1{16}=\dfrac3{16}$ of the whole triangle.
Next smallest shaded triangles: $\dfrac14$ of $\dfrac1{16}=\dfrac1{64}$

That means the shaded triangles of this size occupy $3\times\dfrac1{16}=\dfrac3{16}$ of the whole triangle.
Smallest shaded triangles: $\dfrac14\times\dfrac1{64}=\dfrac1{256}$

That means the shaded triangles of this size occupy $3\times\dfrac1{256}=\dfrac3{256}$ of the whole triangle.
So the total shaded area is $\dfrac14+\dfrac3{16}+\dfrac3{64}+\dfrac{3}{256}$
$=\dfrac{64+3\times16+3\times4+3\times1}{256}\\
=\dfrac{127}{256}$
