Growing Surprises
Can you find the connections between linear and quadratic patterns?
Problem
Growing Surprises printable worksheet
Take a look at the pattern below:

Can you describe the next few patterns in the sequence?
Can you work out how many squares there are in each pattern?
Is there a quick way to work out the number of squares in the 20th pattern? Or the 50th pattern? Or...
Here's another pattern made from squares:
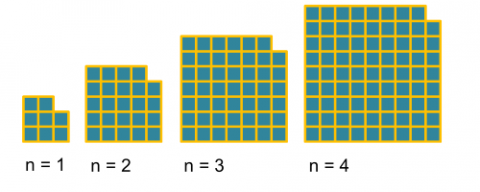
Can you describe the next few patterns in the sequence?
Can you work out how many squares there are in each pattern?
Is there a quick way to work out the number of squares in the 20th pattern? Or the 50th pattern? Or...
Can you describe any relationships between the two patterns?
Here are two similar linked patterns:

Can you find a quick way to work out how many squares there are in these patterns?
Can you describe any relationships between these two patterns?
You may wish to look at some similar problems, Seven Squares, Attractive Tablecloths and Steel Cables.
With thanks to Don Steward, whose ideas formed the basis of this problem.
Student Solutions
Thank you to everybody who submitted solutions for this problem. Here's how some of you thought about the problem:
Tor, from Harbinger School, UK, and Edi, Joseph, Vladimir and Alastair, from The British International School of Shanghai Puxi, China, had a similar approach to the first part of the problem:
I first found the total number of squares in each pattern, and then computed the differences between them. So, the totals are: 8, 16, 24, 32, ... Therefore, the difference between any 2 neighbours is 8, so the $n^\text{th}$ pattern has $8n$ squares.
Then I can easily work out the number of squares in the $ 20^\text{th}$ pattern (there are $8$ x $20 = 160$ squares) or in the $50^\text{th}$ pattern ($8$ x $50 = 400$ squares).
Abby and Rebecca, from the British International School, Shanghai, Puxi campus, and Rosie Coward, from Wycombe High School, England, worked out the formula for the second pattern:
Taking the next sequence, we realised that these were the same shapes, but filled in, rather than hollow. We counted each number of squares from the first patterns, and worked out the differences between each neighbour. Then we did that again, with the new sequence:

So the second difference is 8. Since to find the multiplier (coefficient) of the squared number, you must divide the second difference by two, we found the first term, $4n^2$. Comparing this new sequence $(4, 16, 36, 64)$ to our original one gives a difference of $4n$. Therefore, the number of squares in the $n^\text{th}$ pattern is $4n^2 + 4n$.
From there we found the next 3 terms (120,168, 224), and then found the 20th term (1680)
and the 50th (10200).
Tim, from Gosforth Academy, UK, used a geometric approach to the problem:
Each shape consists of two $2n-1$ sides (the left and right ones, in green) and two $2n+1$ sides (the top and bottom ones, in pink). The diagram shows the $n=6$ case:

Therefore, the total number of squares in the $n^\text{th}$ pattern is $2(2n+1) + 2(2n-1) = 8n$.
Interestingly, if we fit the pieces into each other, we get the solid shapes shown in the second sequence:

From before, $A_n = 8n$ for each $n$. Hence, $B_n = 8 (1 + 2 + ... + n)$.
But $1+2 +...+n$ is the $n^\text{th}$ triangular number. So, $B_n = 8$ x the $n^\text{th}$ triangular number.
This makes sense geometrically:

Using the formula for the $n^\text{th}$ triangular number we get: $B_n = 8 n (n+1)/2$, so $B_n = 4n(n+1) = 4n^2 + 4n$.
Michael and Lera, from Harbinger Primary, UK, expressed it in a slightly different way.
In the second sequence, each pattern is obtained from the previous one in the sequence, plus a contour from the first sequence:

Nia from School No. 97, Bucharest, Romania, created the next two patterns in each of the first two sequences, and gave a slightly different gometric interpretation:
The next two patterns (the fifth and sixth) in the first and second sequences are:

The second pattern could be described as a full $2n+1$ by $2n+1$ square, with the top right $1$ by $1$ square missing. Therefore, the number of squares is $(2n+1)\times (2n+1) -1$.
The first pattern, consists of the contour of each of these squares with the top right corner moved down diagonally. If we firstly move the top right square such that we get the contour of a $2n+1$ by $2n+1$ square, we get:


Now the number of squares are easy to count: there are four groups of $2n$ squares, so there are $8n$ squares.
Alternatively, each is the contour of an $2n+1$ by $2n+1$ square so is a $2n+1$ by $2n+1$ square with the centre (a $2n-1$ by $2n-1$ square) missing. So the area is $(2n+1)^2 - (2n-1)^2 = 4n^2 +4n + 1 - 4n^2 + 4n -1 = 8n$, the same result as before.
Ryan, from The British International School, Shanghai Puxi, China, found a relationship between the first and the second pattern:
The areas in the first sequence are $8, 16, 24, 32, ...$, while the ones in the second pattern are $8, 24, 48, 80, ...$. Now, if we divide the numbers from the second sequence by the ones in the first we get $1, 1.5, 2, 2.5, ...$. Hence, the areas in the second sequence are obtained from the ones from the first sequence by multiplying them by $0.5n + 0.5$.
This is consistent with the algebra: $4n^2 +4n = 8n (0.5n+0.5)$.
Abby and Rebecca, also from The British International School, Shanghai, Puxi campus, China, found a different relationship:
The first few terms of the first sequence are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
The first few terms of the second sequence are 8, 24, 48, 80, 120...
We realised that the first numbers are the same in both the first and the second sequence.
The second number from the second sequence is the same as the third number in the first sequence.
The third number in the second sequence is the same as the sixth from the first.
And so on...
The second sequence is obtained from the first by skipping one number then two, then three...
Also, the difference between the two sequences is $4n(n-1)$.
Angela, Jessica, Brian,Frank, Abby and Rebecca, from The British International School, Shanghai, Puxi, China, have identified the number of squares in the next pair of patterns:
As we looked at the next two, we found that the same pattern occurred: the
first (linear) sequence was simply the outside 'layer' of the other (quadratic) sequence.
By counting squares, we get that the first sequence is $8, 14, 20, 26, ...$. The difference between two consecutive terms is $6$, so the $n^\text{th}$ pattern has $6n+2$ squares.
For the last sequence, we do repeated differences between consecutive terms again:

We divide $4$ by $2$ to get the coefficient of $n^2$: so we have $2n^2$. Then we subtract $2n^2$ from the original sequence for each term and we get $6, 10, 14, 18, ...$. The difference between two consecutive term is $4$, so $n$ has a coefficient of $4$. Therefore, the $n^\text{th}$ pattern of the sequence has $2n^2 + 4n + 2$ squares.
As we looked at them, we realized the reason why one was linear while the other one was quadratic. The first one was counting squares on the contour, which is simply finding the perimeter. The second one was finding the area of an almost full square, so it should have an $n^2$ term. In other words, the perimeter has only one dimension, while areas have two dimensions.
Nia from School No. 97, Bucharest, Romania, approached this part of the problem geometrically:
By moving the yellow squares from the picture below diagonally up, we can see that the first pattern is obtained from the contour of an $2+n$ by $2n+1$ rectangle. The diagram shows the $n=4$ case.

So the number of squares in the pattern is the same as in the contour of an $n+2$ by $2n+1$ rectangle, and hence, we can count the squares:

Alternatively, from the area of an $n+2$ by $2n+1$ rectangle, which is $(n+2) \times (2n+1)$, subtract the area of a $n$ by $2n-1$ rectangle, which is $n(2n-1)$. Therefore, the contour has $(n+2) \times (2n+1) - n(2n-1) = 6n +2$ squares for each $n$.
Yet another way of doing it was to compare this pattern with the one in the first sequence. We can construct one from another as shown in the figure below, again demonstrating the $n=4$ case:

The last pattern is made from a $n+1$ by $2n+1$ rectangle (in blue) with a $1$ by $n+1$ (in red) rectangle on top. So in total, it has $(n+1)\times (2n+1) + 1\times (n+1) = 2(n+1)^2$.

Emma, Inés and Eline from King's College, Alicante, Spain, approached the last part of the problem slightly differently:
We divided the pattern into two rectangles: The area of the first one (in red) would be $(n+1)(n+2)$, while the area of the second one (in blue) would be $n(n+1)$. The diagram shows the case where $n=4$.

Emily Powell, from Hymers College, England, and Vladimir and Joseph, from The British International School, Shanghai Puxi Campus, completed the rectangle instead of breaking it up:
In the second sequence we know that the number of squares missing is always equal to n. So we can add an $n$ by $1$ rectangle to our pattern (in red below) so that we get a complete $(n+2)$ by $2n+1$ rectangle. The diagram shows the case where $n=4$.

Sameer and Will, from Hymers College, England, noticed something different:
We know that the contour has $6n + 2$ squares. Then we can break the inside into two halves, as below:

Hence, the area of the interior part is $2n(n-1)$. We then add the area of the contour, to get the area of the whole pattern: $2n(n-1) + 6n+2 = 2n^2 +4n +2 = 2(n+1)^2$.
Well done to you all for sending such a variety of solutions!
Teachers' Resources
This printable worksheet may be useful: Growing Surprises.
The worksheet is also available in French: Suites Surprises.
We are grateful to Clara Huizink for translating the original.
Why do this problem?
The geometric representation of sequences in this problem gives students something concrete to work with as they begin working with quadratic sequences. As well as introducing or consolidating sequences expressed term-to-term or position-to-term, this problem offers a chance to gain fluency in creating and manipulating algebraic expressions and recognising equivalence.
Possible approach
Squared paper and mini-whiteboards could be useful.
Show students the first sequence of patterns. Check that they can draw the next pattern in the sequence. How did they know what it would look like?
Next, ask students to count the number of squares in each shape. Is there a rule? Is the number pattern (+8 each time – they are likely to spot the term-to-term rule, rather than a rule for the $n$th term) related to the geometric rule (add 2 more squares to each side of the shape)? Allow some time for students to work alone or in small groups, and then to share their work with the class.
Then ask students how many squares there would be in the 20th pattern, or the 50th pattern. Let them work alone or in small groups so that you end up with a variety of methods and ideas. You could encourage students to focus on the geometric representation by suggesting they sketch the 20th pattern – how long will the sides be? You could suggest that they make a table showing $n$ and the number of squares in the $n$th pattern to encourage them to find a position-to-term rule. Students can then extend their reasoning to the 50th pattern, and so on, and generalise to the $n$th pattern.
Several different representations are likely to arise, and so this is a good time to share students’ work. Give students time to confirm that their different methods lead to the same results (or to find out why they don’t) and to understand the connections between the representations. You could leave examples of the different methods on the board so that students can refer to them as they move on to the next part of the problem. You might want to agree on some notation at this point.
For the next part, students are likely to feel ready to begin investigating using the representations from the first part. The sequence is a quadratic sequence, and so may be more challenging for students to generalise. As well as the strategies used previously, they may notice that each pattern is a square with one corner missing – or that the number of squares used is always one less than a square number. Some may recognise the sequence as the sum of the patterns in the first sequence.
Once again, several different methods and representations are likely to emerge as students work in small groups. You might want to bring the students together for a whole class discussion to share their work as the end of the lesson, or before moving all students on to the third part of the problem. Alternatively, you could move some students onto the third part once you feel they are ready, and share their findings at the end of the lesson.
Key questions
How are we going to record our findings?
What is the difference between each shape in the sequence?
Can you find a pattern between the position in the sequence and the number of squares in the shape?
How do you know your pattern will continue?
Possible support
Encourage students to draw out the patterns and describe them verbally. Then formalise the description mathematically and introduce a notation in a structured way, possibly by using a table for e.g.
| Position in the sequence | 1 | 2 | 3 |
| Squares in the shape | |||
| Link between position and number of squares |
Possible extension
How many different methods can you find to solve this problem?
