The wisdom of the crowd
Who's closest to the correct number of sweets in a jar - an individual guess or the average of many individuals' guesses? Which average?
Age
11 to 16
Challenge level
Problem
Image
Do you believe that a crowd can be more intelligent than any individual in the crowd?
Find out with an easy experiment!
Fill a jar with jelly beans (or similar small items) and ask as many people as possible to guess how many there are.
Count the jelly beans, and give them to the person whose guess is closest, but keep the record of all the guesses made.
How close was the best guess?
How far off were the worst guesses?
Were there more guesses below the actual number or above it?
How far off were the worst guesses?
Were there more guesses below the actual number or above it?
It's often the case that the crowd is better at guessing than the individuals in it! Don't believe it?
Calculate the average number of guesses - you could calculate both the median and the mean.
How close are they to the actual number?
How many people did better than the median?
How many people did better than the mean?
How many people did better than the median?
How many people did better than the mean?
So who was wiser here - the crowd (as represented by the averages) or individuals?
Image
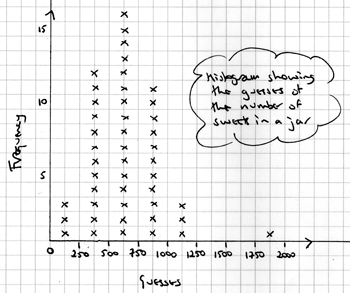
Now display the guesses in a graph. It's easy to build up a histogram, using squared paper:
- put sensible intervals along the horizontal axis
- for each guess, put a small cross in squares in the centre of each interval, so that you build up a column for each interval (as on the right)
Or is it skewed to the left or the right?
The graph shown here is skewed to the right (by one particularly large guess).
Teachers' Resources
Why do this problem?
This problem provides an experimental context in which students can compare the advantages of the median and mean averages as data summaries, while investigating an interesting phenonmenon - that in some cases, a crowd acting as individuals often make better decisions than the individuals of which it is made.
Possible approach
Provide a transparent container which is full of small sweets or other small items - there should be too many for anyone to be able to estimate how many there are at all easily.
Tell the students to survey as many people as possible, asking them how many sweets they think the container contains. Students should keep a record of the guesses (with names, if sweets are involved, so that the winner can receive their prize!), then calculate the median and mean average.
Key questions
How close are the averages to the actual number of sweets in the container?
How many people guessed closer than the averages?
Which is the best estimate - a guess, or an average, and if so, which average?
Possible extension
Students could build up a simple histogram to display the guesses graphically. They should then consider what the distribution of guesses looks like.
What is the overall shape? How do you explain this shape?
Which intervals received most guesses, which least?
Are there any particularly extreme guesses?
How symmetrical is the distribution?
The distribution is likely to be skewed, because people are less likely to make extreme under-estimates than over-estimates when guessing like this.
This means that the distribution may well not be symmetric, and that therefore the median and mean will be different - a point worth drawing to the students' attention.
The median is not affected by the value of extreme guesses, simply by the number of them, whereas the mean is affected by their value as well as their number.
The geometric mean gives the best estimate for the actual number of sweets in the container, and this could be a further extension.
Possible support
The most difficult aspect is ensuring that students don't make mistakes in calculating the mean and median if there is a lot of data. It may help to provide a tablet or laptop so that data can be entered directly into a spreadsheet, and any calculations which are done by hand can then be checked against the spreadsheet answers.
Alternatively, students could be given a small subset of the data to analyse by hand, then the data set as a whole analysed with the spreadsheet for further discussion.