Interior Squares
Calculate the ratio of areas of these squares which are inscribed inside a semi-circle and a circle.
Problem
Image
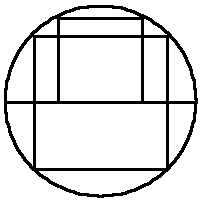
The diagram shows a square of area $x$ square units inscribed inside a semicircle and a larger square of area $y$ square units inscribed inside a circle.
What is the ratio $x : y$ ?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Image
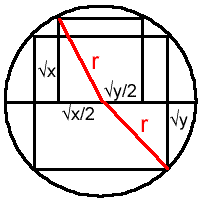
Let $r$ be the radius of the circle, then for the smaller square we can apply Pythagoras' Theorem:
$r^2=(\sqrt{x})^2+(\sqrt{x}/2)^2=x+x/4=5x/4$
and for the larger square:
$r^2=(\sqrt{y}/2)^2+(\sqrt{y}/2)^2=y/2$
So $x:y = 2:5$.
