Two Clocks
These clocks have only one hand, but can you work out what time they are showing from the information?
Problem
This problem could be worked on in a group of about four. For more details about how you might go about doing this, please read the Teachers' Notes.
Sam and Julie are friends. Both of them have rather odd clocks at home.
In Sam's bedroom there is an old alarm clock which his Dad had thrown out because it had lost its minute hand. Although it has only its small hand, Sam can still tell the time using it. He can tell the hour, such as midday. He can tell when it is time to get up, time to go to school and time to turn his light out at night.
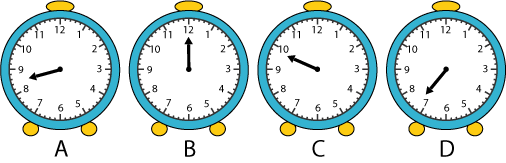
Which clock is showing it is midday?
At what time does Sam get up?
At what time does Sam go to school?
At what time is Sam supposed to turn out his light?
In Julie's hall there is a very old clock which lost its hour hand a long time ago.
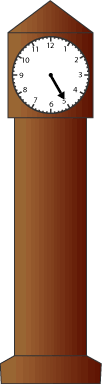
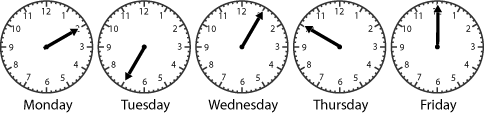
School finishes at half past three and it takes Julie at least half an hour to get home. Sometimes she goes to the shop on the way, and sometimes she leaves school a bit later. When she first gets home Julie always looks at the clock in the hall to see what time it is.
One week these were the times she saw:
Getting Started
Approximately what time do you think each clock is showing?
Can you order these times together to fit in with Sam's day?
Thinking about Julie's week, where might the minute hand of the clock be if she hurries home from school and it takes about half an hour?
Which three clocks show minute hands five minutes apart? Might that help you to decide which days they were?
Student Solutions
Thank you to everybody who wrote in to tell us what they thought about these clocks. Most children agreed on the answers, and it was interesting to see the different reasons that children gave.
We received a lot of solutions from the children at King's Hedges. Yousuf and Daniel explained their ideas:
D is what time he wakes up as it is the earliest time (7:15). A is the time he gets to school as 8:30 is the average time to go to school and is the second earliest time. B is midday as 12:00 is midday and no other clock shows 12. With process of elimination, that makes C when he turns his lights off (21:45).
On Friday, she went straight home as 30 minutes past 3.30pm is 4. Wednesday she stayed for 5 minutes so it'd be 4.05pm. Tuesday is when she played with a friend as it's 4.35pm and it said she played for around 30 minutes. On Monday, she bought sweets as it doesn't take 50 minutes to get sweets on the way home. Therefore, Thursday is band practice.
I like the way you showed the order in which you answered these questions - often it is easiest to answer one of the questions using a 'process of elimination'! We were also sent in similar solutions by Zoe, Blanka, Mason, Adrian, Robert, Dominika and Neve at King's Hedges - thank you for sharing your ideas with us.
We also received several solutions from the children at Norwest Christian College in Australia. Nathan thought that the hands on the first set of clocks were pointing to the small lines, rather than splitting the hour into quarters:
Part 1:
Each clock interval for the hour clock is 12min so that means:
A Clock: 8:30 (am/pm)
B Clock: 12:00 (am/pm)
C Clock: 9:48 (am/pm)
D Clock: 7:18 (am/pm)
I think D is waking up, just out of personal experience, I think A is going to school because my school starts at 8:35, so getting to school at 8:30am would be the best time, I think C is lights out because around 9:48pm is about the time when I would go to bed, I think that B is of course midday. I think this question is mostly based off your lifestyle and what time school is for you.
Part 2:
If schools ends at 3:30pm and it takes her 30min to get home at least, she must get home at 4pm at the earliest, so when she runs home quickly that means that since the Friday clock is on 4 o’clock, that means that she ran home quickly on Friday. Since the teacher kept the class in for 5min after school and she rushed home, that means that she would get home at 4:05pm, which is the clock of Wednesday. When she went to play with Sam for about half an hour, that means that the clock should show about 4:30pm, and the Tuesday clock does, so she played with Sam on Tuesday. This is where it starts getting harder, we don’t have a time or how long things took, so we need to guess, from past experiences, going into the shops to get some snacks doesn’t take that long, so I believe that it only takes about 10min to get it, and that’s what the Monday clock says, so I believe that she went and picked up lollies on Monday. Now, since there is only now one more clock left, it means that the Thursday clock must be the band day.
Well done for using your own personal experiences to put these events into context! Aarnav, Lucas, Diya and Chloe from Norwest Christian College also had some similar ideas.
The children at St Helen's Abbotsham in England sent in their ideas about these questions. Albie, Olivia, Edgar and Sonny said:
Question 1:
B=Mid day because the hand is pointing to the twelve.
D=When he wakes up because school starts at 08:30 so you can't wake up at nearly ten!
A=When he goes to school because I don't think school would start at nearly ten!
C=When he goes to bed because it's too late for school.
Question 2:
Monday (1610) we think is when Julie gets sweets because it takes about 10 minutes to buy sweets.
Tuesday (1635) we think is playing with Sam because it is 4 o'clock plus a half hour.
Wednesday (1605) we think is staying in for five minutes because 30+5=35
Thursday (1650) is band practise 45+30 plus faffing time
Friday (1600) is where she rushes home, taking 30 minutes.
Sam, Ralph, Molly, Amélie, William, Lucy, Amelia, Rosie, Frances, Kacie, Myles, Reuben, Adam, Riley, Aiden, Tommie, Ophelia, Amber, Charlie, Neda, Fraser, Joanne and Oliver from St Helen's Abbotsham also sent in some similar solutions. Thank you all for sharing your ideas with us.
Gabriel and Muhammad from Wembrook Primary School sent in their ideas about these questions. Gabriel said:
Wednesday could be the day that the teacher kept the class in for 5 minutes because she comes home usually at 4:00 and 4:00 + 5 minutes = 4:05.
Thursday could be the day that she practised in the band because the times just tells us that it's XX:50 so it could be 3:50 or 4:50.
Friday could be the day that she hurried straight home because it takes her 30 minutes to get home at least.
Monday can be the day she goes to get sweets.
That leaves Tuesday being the day that she plays with Sam.
Good ideas - how do we know that the time that shows XX:50 can't be 3:50?
Lucy and Ryan from Bishop’s Castle Primary School in the UK had some similar ideas and they used number lines to show how they thought Julie might have spent her time on her way home from school. Ryan sent in this picture:
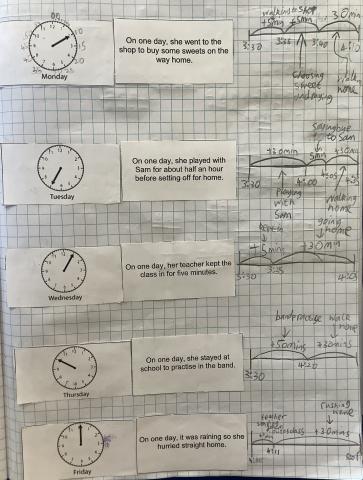
This method makes it really easy to see where she might have spent some extra time on each day. This is similar to Albie, Olivia, Edgar and Sonny's idea about 'faffing time' - if your home is a 30 minute walk from school, I'm not sure how likely you are to actually get home 30 minutes after school finishes!
Unfortunately we don't have space here to include all the solutions we were sent. We also received excellent solutions to this activity from: Will from P.S.24 in the USA; Chloe, Sophia, James, Zac, Milan, Harry and Dray from Banstead Prep School in England; Om from St Leonard, Exeter in the UK; Sasha from Bilingual International School of Paris in France; Koen from KPS in Scotland; Ci Hui Minh Ngoc from Kelvin Grove State College in Brisbane, Australia; Dhruv from The Glasgow Academy in the UK; and Meriam and Millie.
Josh from Banstead Prep School thought that there could be multiple possible solutions to the first part of the problem:
C shows it's 9:45 since it's $\frac{3}{4}$ of the way to the 10. This can be multiple answers. It can be when he goes to school or when he turns out the light.
D shows 7:15 since it is $\frac{1}{4}$ past the 7 but it could be when he wakes up or when the lights go out.
Good ideas, Josh. I wonder how many different possible answers there are to the first part of the problem, thinking about clocks A, C and D. The only thing we know for definite is that Sam goes to school after he gets up in the morning, not before! I suppose the rest of the solution mostly depends on how much sleep he needs.
Teachers' Resources
Why do this problem?
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Possible approach
- Every group is given a couple of minutes to report back to the whole class. Learners can seek clarification and ask questions. After each presentation, children are invited to offer positive feedback. Finally, pupils can suggest how the group could have improved their work on the task.
- Everyone's posters are put on display at the front of the room, but only a couple of groups are selected to report back to the whole class. Feedback and suggestions can be given in the same way as above. Additionally, children from the groups which don't present can be invited to share at the end anything they did differently.
- Two children from each group move to join an adjacent group. The two "hosts" explain their findings to the two "visitors". The "visitors" act as critical friends, requiring clear mathematical explanations and justifications. The "visitors" then comment on anything they did differently in their own group.
You may find that there is not agreement on the 'final' solution. The important thing is that each group can justify its reasoning. This may lead to a consensus amongst the whole class, but it may not.
Key questions
Possible extension
Those who already tell the time efficiently could write the time when various activities take place at school on both one-handed clocks.
Possible support
Some children find telling the time with analogue clocks extremely difficult. A (one-handed) model clock would be very useful at this point.
