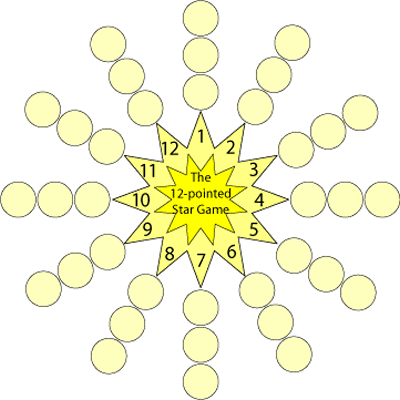
The twelve pointed star game
Have a go at this game which involves throwing two dice and adding their totals. Where should you place your counters to be more likely to win?
Problem
This game is for two or more players.
You will need a copy of the star board, counters and two 1-6 dice.
Each player chooses three numbers on the star. (If you play with more than four players, each player chooses two numbers.)
Players then take it in turns to roll two dice and add the scores.
The player who has chosen that number puts a counter on the appropriate circle.
The winner is the first player to have counters on all three circles belonging to one of their chosen numbers.
For example I'm playing with my friend Zac. I choose the numbers 2, 4 and 6; Zac chooses 7, 8 and 9.
Zac rolls the dice and it's a 4 and a 2, which makes a total of 6.
This means I can put a counter on one of the circles next to the 6.
Play the game a few times.
Which are good numbers to choose? Why?
Which are poor numbers to choose? Why?
Which is the worst number to choose? Why?
Getting Started
You could try playing the game a few times first.
What totals are possible when you roll two dice?
How many ways can you make each of these totals?
Student Solutions
Congratulations to Cong Lu from Aberdeen , Keshav from Singapore, Fionne from Leiston, George from St Nicholas C of E Junior School and Luke from Wirral Grammar School for Boys who all sent in correct solutions.
George's solution is given below:
We all played the game in pairs and then looked at which were the winning numbers.
The best numbers (the numbers that won the most times) were 6, 7, 8, 9 and 10.
The best numbers to choose are 6, 7 and 8 because they have the most combinations.
When we played this game, the worst numbers (the numbers which lost the most times) were 2, 3, 4, 5, 11 and 12. These are poor numbers to choose because they don't have many combinations.
Teachers' Resources
The Twelve Pointed Star Game
This game is for two or more players.
You will need a copy of the star board, counters and two 1-6 dice.
Each player chooses three numbers on the star. (If you play with more than four players, each player chooses two numbers.)
Players then take it in turns to roll two dice and add the scores.
The player who has chosen that number puts a counter on the appropriate circle.
The winner is the first player to have counters on all three circles belonging to one of their chosen numbers.
For example I'm playing with my friend Zac. I choose the numbers 2, 4 and 6; Zac chooses 7, 8 and 9.
Zac rolls the dice and it's a 4 and a 2, which makes a total of 6.
This means I can put a counter on one of the circles next to the 6.
Play the game a few times.
Which are good numbers to choose? Why?
Which are poor numbers to choose? Why?
Which is the worst number to choose? Why?
Why do this problem?
This game offers a good context in which to explore possible outcomes and to think systematically about what scores are possible. It will be important for learners to develop a recording or listing system that they are happy with, in order to find all the possible ways in which the different totals can be made.
Possible approach
You could start by encouraging the group to try playing the game a few times and then pool their results of 'winning numbers'. It is not necessary to have the star or counters - you could just write the numbers $1$ to $12$ on a piece of paper and put ticks against the numbers that come up. However, it is more appealing to use the star. Here is a coloured copy of the board which could be printed off for pupils to use and here is one in black and white that can be photocopied.
Which are good numbers to choose? Why?
Which are poor numbers to choose? Why?
Which is the worst number to choose? Why?
Key questions
Possible extension
Pupils could be challenged to make a version of the game which was fairer.
Possible support
Some children will find it useful to manipulate dice as they work out the possible outcomes.