Pythagoras for a Tetrahedron
|
Consider a right-angled tetrahedron with vertices at $O(0,0,0)$, $A(a, 0, 0)$, $B(0, b, 0)$ and $C(0, 0, c)$.
Let the area of face $AOB$ be $P$, the area of $BOC$ be $Q$ and the area of $COA$ be $R$. Also let the slanted face $ABC$ have area $S$.
($S$ is not shown on the diagram above!). Can you prove that $P^2+ Q^2+ R^2= S^2$?
|
Equivalently: (area $OBC$)$^2 + $(area $OCA$)$^2 + $(area $OAB$)$^2 = $(area $ABC$)$^2$.
Extension
If you enjoyed this question, you might like explore STEP Support Programme Foundation Assignment 5 which asks a question about the perpendicular distance of face $ABC$ from the origin.
There are a few different approaches you can try.
- You could use Heron's formula for the area of a triangle.
- You could use $\tfrac 1 2 ab \sin C$ for the area of a triangle. It might be helpful to remember that $\cos^2 \theta+\sin^2 \theta = 1$.
- You could try and find a point $X$ on $AB$ such that $CX$ is perpendicular to $AB$, and then use $\tfrac 1 2 bh$ for the area of a triangle. Vectors might be useful here, as well as the fact that ${\bf p}\cdot {\bf q}=0$ if and only if the vectors ${\bf p}$ and ${\bf q}$ are perpendicular. There are quite a lot of perpendicular vectors in this question!
Thanh from Delta Global School in Vietnam, and Ashil and Hadi from St Dominics 6th Form College, Joshua from Bohunt Sixth Form and Lisa, all from the UK, found the sides of triangle $ABC$ in terms of $a, b$ and $c.$ Joshua, Hadi and Ashil then used the cosine rule, and the formula $Area=\frac12ab\sin C.$ This is Ashil's work (click to enlarge):
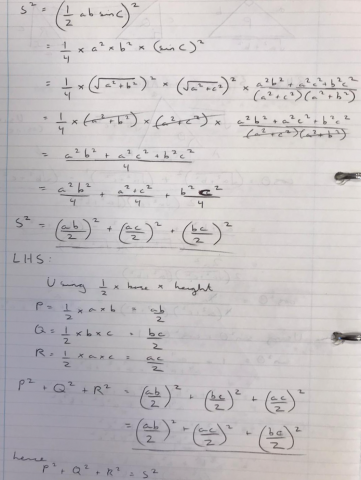
Thanh began in the same way, but then used a perpendicular 'height' to find the area $S$ (instead of the formula):
Lisa used Heron's formula to find the area $S,$ which gave some very neat algebra. Heron's formula works like this: $$\begin{align}&\text{If a triangle has sides }a,b,c\\ &\text{Let }s=\tfrac12\left(a+b+c\right)\\ &\text{then the area of the triangle is equal to }\\ &\sqrt{s(s-a)(s-b)(s-c)}\end{align}$$Here is Lisa's work (click to enlarge):
Yash from Tanglin Trust School in Singapore and Leo from Stowe School in the UK both took a more algebraic approach. Most of ther work is exactly the same, but they started in subtly different ways. Yash began:
Note that Yash's equation is not true: for the area $P$ to be equal to $\frac12\times AB \times DO,$ $AB$ and $DO$ need to be perpendicular. However, they may not be. This means that Yash has made an unjustified assumption.
Leo defined point $D$ (or point $X$) in a different way, which means that Leo didn't need to make this assumption:
Yash and Leo then proceeded in the same way as each other. Here is the rest of Leo's work:
Why use this problem?
The problem introduces an attractive generalisation of Pythagoras' theorem to 3D.
There is the opportunity to explore different solution techniques. Some methods include:
- Using the area of a triangle formulae and Pythagoras's theorem.
- Using Heron's formula.
- Using vectors.
Key questions
What information is given?
In what different ways could we find the area of a triangle?
What can be deduced from the geometrical properties?
What are the unknowns and what notation shall we use?
What equations can we write down for the areas of the four triangular faces of the tetrahedron?
What equations can we write down involving the lengths of the edges of the tetrahedron?
How can we put all this together to get the required result?
Possible support
Try the problem Rectangular Pyramids.
Possible extension
Try using different methods to solve the problem.
Generalise the result to a cosine rule for a tetrahedron.
STEP Support Programme Foundation Assignment 5 asks a different question about the same tetrahedron.