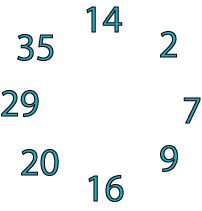Cycling Squares

Can you make a cycle of pairs that add to make a square number using all the numbers in the box below, once and once only?

Age

7 to 11

Challenge level

Primary

Number - Multiplication, Division and Ratio

Properties of Numbers: Multiples, Factors, Primes, Square and Cube Numbers

Exploring and noticing Working systematically Conjecturing and generalising Visualising and representing Reasoning, convincing and proving

Being curious Being resourceful Being resilient Being collaborative

Problem

In the circle of numbers below each adjoining pair adds to make a square number:

For example,

$14 + 2 = 16, 2 + 7 = 9, 7 + 9 = 16$

and so on.

Can you make a similar - but larger - cycle of pairs that each add to make a square number, using all the numbers in the box below, once and once only?

You might find it helpful to print off and cut up these cards of the numbers so you can move them around to try out your ideas.

Student Solutions

William from Tattingstone School said that he tried four times before he came up with a solution to Cycling Squares:

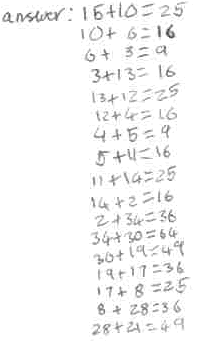
We're glad you didn't give up, William. Beth and Pheobe from Exminster CP School and Skye and Molly from Breckland Middle School also used trial and error (or trial and improvement as I like to call it!). Beth and Phoebe said it tested their skills of perseverance.

Matha, also from Tattingstone, said that she started with the number $2$ and then added $14$ because it was the only number she could have added to make a square number. She goes on to say:

I then added $11$ to $14$ to get $25$ which is another square number and carried on like this.

Martha sent in a drawing of her circle which is the same as William's answer, just written in a different way:

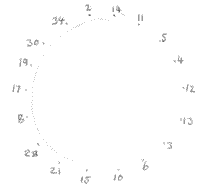
Dominic from Stonehill took a logical approach:

I listed the numbers and wrote down their pairs to make square numbers.

Some of the numbers only had two possible combinations to make square numbers, so I started with one of these. I put in $2$ first and put $14$ and $34$ on either side of it.

From there, I put $11$ on the other side of the $14$ as these were the only combinations, and so on.

Some numbers had four or even five possible combinations but by trial and error I moved these around until all the combinations made a square number.

Brandon, Antonia and Oliver from Mayhill Junior used a similar method to Dominic. Emilie and Bethany from Alverstoke Junior School said:

To solve the problem we first worked out the highest square number was $64$.

We then worked out all the square numbers from $4$ to $64$.

We then worked out which pairs of numbers made square numbers and we used trial and error to solve the problem.

Very well done to you all. Here are some comments we received in 2015 from pupils at Queen Edith, Cambridge having completed the challenge.

Edward:- "I worked it out by using trial and improvement and it took us a couple of times to figure it out. I started with one pair of numbers and went both ways around the circle"

James:- "I worked out what numbers added together which would make a square number. Next we put two adjoining numbers to make a square number and we used trial and improvement to work out which number came next"

Lavinia:-" We worked together and persevered. If we got it wrong, we helped each other to make the answer right. Cooperating we completed the challenge even though it was hard!

Abigail :-"Clare and I chose the biggest number that was available in the range and made the first possible number that we could think of: 64 (30 + 34) We found out putting 34 first did not work so we put 30 first. We worked our way around the circle clockwise using trial and improvement to complete the challenge!

Lauren :-"Even though it was tricky we still persevered and tried our best. I had to use trial and improvement to make the circle but the best thing was to have fun!

Thank you Queen Edith pupils it made interesting reading. Well Done!

Teachers' Resources

Cycling Squares

In the circle of numbers below each adjoining pair adds to make a square number:

For example,

$14 + 2 = 16, 2 + 7 = 9, 7 + 9 = 16$

and so on.

Can you make a similar - but larger - cycle of pairs that each add to make a square number, using all the numbers in the box below, once and once only?

You might find it helpful to print off and cut up these cards of the numbers so you can move them around to try out your ideas.

Why do this problem?

This problem is a challenging one. It uses the learner's knowledge of square numbers and gives the opportunity of practising addition in an unusual context. It is a useful problem through which to discuss different methods of approach.

Possible approach

You could start by reminding the group about square numbers, perhaps by playing a game of 'I like ...' where you write up numbers you 'like' (i.e. are part of a set) to one side of the board and numbers you 'don't like' (i.e. are not in your set) to the other, as children suggest numbers. The idea is for children to determine the name of your set.

You could then use the small cycle given at the beginning of the problem to introduce the idea of a cycle of squares, encouraging learners to check that each pair of numbers does indeed add to a square number.

(The cycle goes like this: 14 - 2 - 7 - 9 - 16 - 20 - 29 - 35 -.)

Then you could go on to introducing the actual problem. Learners could work on this in pairs, using numbered counters that can be moved round experimentally or number cards printed from this sheet.

At the end of the lesson, all learners could be involved in a discussion of how they tackled the problem, building up the cycle on the board, number by number. You could invite them to comment about the advantages/disadvantages of the different methods used and they may decide that one method is particularly efficient.

Key questions

Can you think of a good way to start?

Have you made a list of square numbers up to 100?

Which of the numbers given can be added to that one to make a square number?

If you cannot go on from there, what could you try instead?

Possible extension

Learners could make their own cycle of squares using different numbers, or invent cycles using a different number property.

Possible support

Making a list of the square numbers up to 100 will help some children get started on this problem. Encourage the learner to choose one number and see which of the numbers given can be added to it to make a square number. Numbered counters to work with could be very helpful and a calculator might free-up some children who find calculation difficult.

Or search by topic

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Cycling Squares

Problem

Getting Started

Student Solutions

Teachers' Resources

Cycling Squares

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support