Square Corners
What is the greatest number of counters you can place on the grid below without four of them lying at the corners of a square?
Problem
Have a look at the three grids below.
What do you see?
What do you notice?
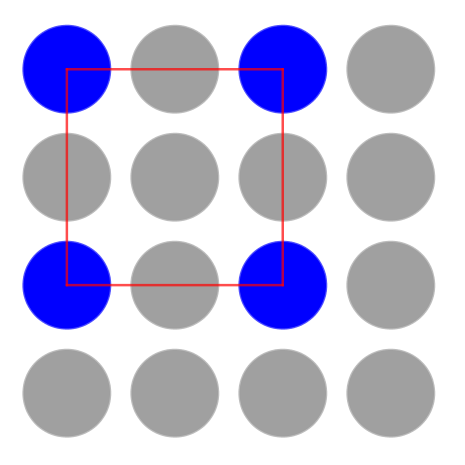
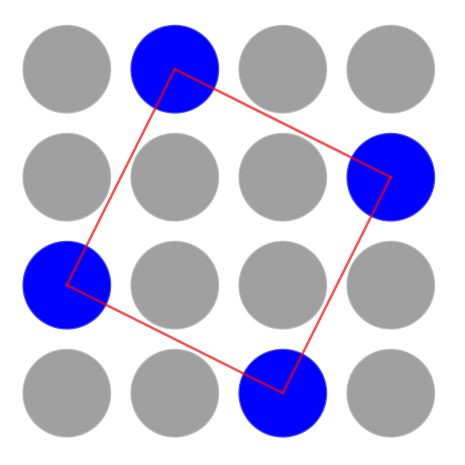
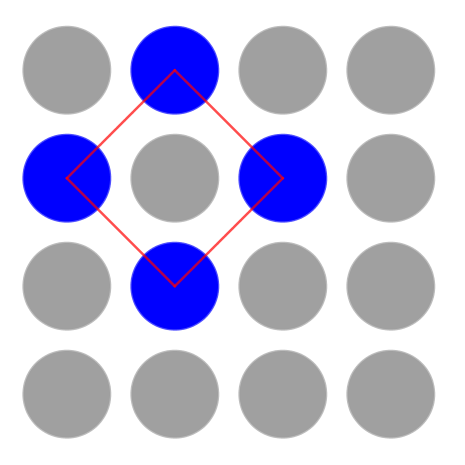
Once you have had chance to think, talk to someone else about your noticings.
Click below to read what some children noticed.
Miles said:
There are lots of spots. And I can see some of the spots are blue. The blue spots are joined to make shapes.
Freya said:
All the shapes have four sides. Some of the shapes are turned round.
Omar said:
I can see three red squares! They're different sizes.
Do you agree with Miles, Freya and Omar? Why or why not?
Now it is your turn...
Use the interactivity below to put blue counters on the grid.
Your challenge is to put as many counters on the grid as you can but none of them must lie at the corners of a square.
How many counters can you use without making a square?
How do you know that you cannot have more counters?
You're doing really well if you can place 8 or 9 counters.
We think 10 is the maximum number possible, but do let us know if you can find a way of placing 11!
If you would prefer to work away from the computer, you might like to use a printable sheet (square grid or array of circles) with counters.
We would love to hear how you are going about this task!
This problem is taken from 'Mathematical Challenges for Able Pupils Key Stages 1 and 2', published by DfES.
Getting Started
One way to start would be to find all the possible places for the four counters to go that would actually make a square.
Or you could fill in the grid with counters one by one, checking to make sure you haven't made a square.
Being systematic (i.e. doing things in a logical order) is the key!
Student Solutions
Well done to everybody who solved this problem! We had lots of solutions telling us that 10 is the maximum number of counters you can place on the grid without making a square. The following solutions came from children who explained their reasoning particularly clearly.
Dhruv, who is homeschooled in the UK, sent in this picture showing one possible solution:
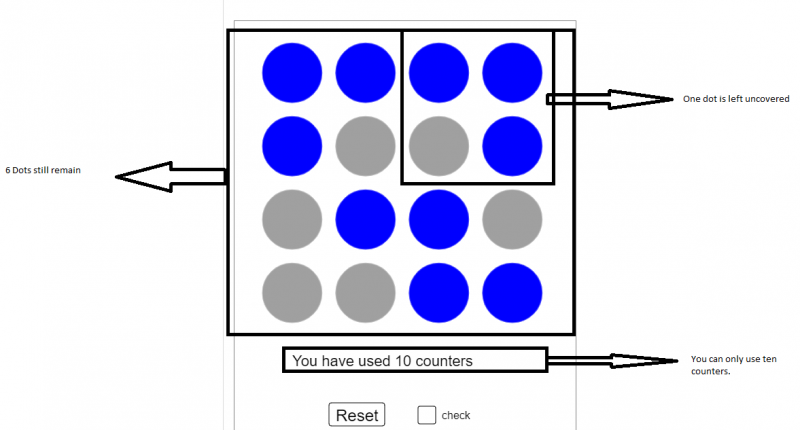
Thank you Dhruv!
Saanvi from Newcastle under Lyme Prep School in England said:
I started by filling in all of the circles and checking how many squares there were and, of course, there were lots. I then chose a point that I think has a large amount of squares coming from it and unselected it. I then repeated the process again and again to find an answer. I found a way of using 9 circles, but then I thought that it might be possible to have more points used, so I tried again and found it that I could use 10 points. I don’t think that it is possible to use 11 because, just to check my answer, I checked every combination of 11 circles and every time found that there were some squares made.
Well done Saanvi - it must have taken you a while to check every combination of 11 circles!
K from Crossflatts in the UK had a similar strategy. Have a look at K's full solution to see the step-by-step process of how they chose which counters to remove at each point. Thank you for sending in this very clear explanation of your thinking, K - we've kept everything you wrote but we've tweaked the format of your pictures to make it easier to read.
We also had some good explanations sent in from: Liam from Furness Academy in England; Milly from Drake Primary School in Thetford; Sachkeerat from Akal Academy Baru Sahib, Himachal Pradesh in India; Anna and Serenade from Sahuaro Elementary Gifted Learning Center in the USA; and Ci Hui Minh Ngoc from Kong Hwa School in Singapore. Thank you all for sending us your solutions.
Charlotte from Halstead Prep School in the UK tried this challenge on a variety of different sizes of grid, and she noticed an interesting pattern:
In a 2 x 2 square I can put three counters. In a 3 x 3 square I think I can put 6 counters. In a 4 x 4 I think 10 and in a 5 x 5 I could put 15. These are part of the triangular sequence and that stops you having squares.
Well done Charlotte, I think you're right - on those grids the answers will be triangular numbers each time. If the pattern continues, I wonder how many counters you could put on a 6 x 6 grid without making any squares? What about a 7 x 7 grid?
Nathaniel from Singapore had some ideas about the number of counters that could be used in a grid of length 6:
I was trying to find the solution for the 6x6 grid and found that 20 squares is possible. I filled in all, then removed each one to see which one removed the most squares. I repeated this until there were zero squares, so I essentially did it by trial and error. I tried adding on 1 more counter and found that it always formed at least 1 square, which makes me think that the maximum is 20. I do think 21 may be possible, but I am not sure.
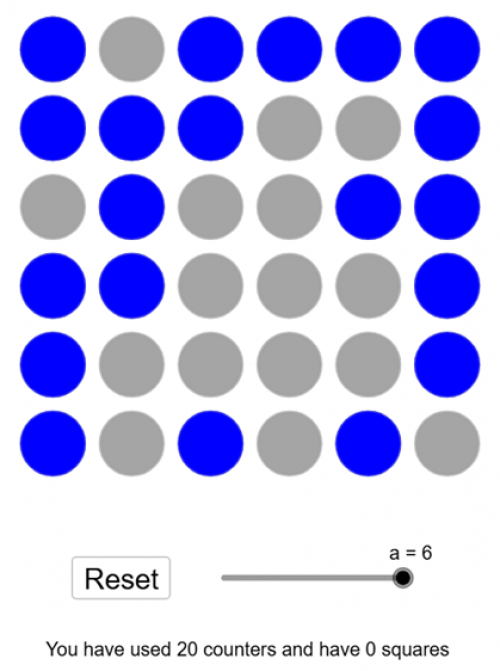
It's very helpful to know that it is possible to complete this version of the challenge using 20 counters. Using Charlotte's pattern, it does look as if it might be possible to find a solution using 21 counters. If anybody finds one, you can email us to let us know.
Teachers' Resources
Why do this problem?
Possible approach
You could begin by playing the game Seeing Squares a few times as a class. This will provoke discussion amongst pupils about what makes a square a square, and you may wish to address the misconception that tilted squares are called 'diamonds'.
Introduce the problem by showing the three images and inviting the class to consider what they see. After talking with a partner, suggest that learners share their noticings. Try to encourage other members of the group to comment on, and question, the observations rather than you validating the contributions. Reveal the three children's comments in the problem and facilitate a discussion so that the class decides whether they agree or disagree with each one.
Using the interactive grid on the interactive whiteboard, help learners to understand the main challenge and ask them to begin to work on it in pairs. If they do not have access to the interactivity on tablets or computers, learners could use a large grid, of squares or an array of circles, with counters and/or this sheet of smaller grids. Remind them to check for squares!
After a suitable length of time, share results so far amongst the whole group. What is the largest number of counters so far? Ask a pair of learners to come up and recreate their arrangement of counters on the screen so that everyone can check there are no squares.
At this point, challenge the class to come up with a way of working that will ensure the largest number of counters is definitely found. How will they know that all arrangements have been tested? Some children may suggest a system based on, for example, placing counters on the grid from top left to bottom right and each time checking that a square has not been made. You could model the beginnings of a strategy and then give the class more time to investigate the problem. It may be that you split the group up to investigate different 'families' of arrangements.
In the plenary, you could discuss the solutions and what makes one arrangement of counters different to another. Will rotations and reflections be considered different or the same?
Key questions
How will you know that you have definitely found the largest number of counters?
Are you sure there aren't any squares on your grid?
Possible support
Possible extension
Children could investigate larger grids and see whether there is a pattern to the number of counters by looking at smaller grids too. Is it possible to predict the largest number of counters in any size grid?
You might like to use the interactivity below to check solutions to larger grid sizes.
