Cyclic quad jigsaw
A picture is made by joining five small quadrilaterals together to
make a large quadrilateral. Is it possible to draw a similar
picture if all the small quadrilaterals are cyclic?
Problem
Someone showed me this picture of a quadrilateral made by joining together five smaller quadrilaterals.
Image
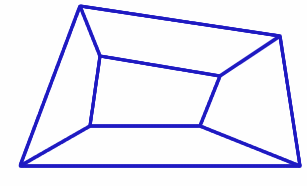
It made me think about special cases...
Could I draw a version of this image where all five of the smaller quadrilaterals are cyclic? I tried it out and have tried to capture what I did, and what the question was that it made me want to answer, in the video below:
Can you convince us that the largest quadrilateral is also cyclic?
Student Solutions
We had two very clear solutions to this problem - well done to James, from Poole Grammar School, and Dylan, who did not give his school. James's solution is shown here.
Image

All five of the small quadrilaterals in the above shape are
cyclic, and by using the fact that opposite angles in a cyclic
quadrilateral add up to $180 ^{\circ}$ we can prove that the large
quadrilateral made up of the five smaller ones is also
cyclic.
Opposite angles in each cyclic quadrilateral add up to
$180^{\circ}$, so we can write expressions for angles $a$, $c$, and
$e$.
$$a = 180^{\circ}- b$$ $$c = 180^{\circ}- d$$ $$e =
180^{\circ}- f$$
Angles $a$, $c$, and $e$ are all round the same point
therefore: $$360^{\circ} = a + c + e$$ Substituting in the
expressions for angles c and e in we get: $$360^{\circ} = a +
(180^{\circ} - d) + (180^{\circ} - f)$$
Simplifying this we get: $$360^{\circ} = a + 360^{\circ} - d -
f$$ $$ a = d + f$$
Now we follow exactly the same working with the other side of
the quadrilateral which gives us the equation $$b = h + j$$
We also know that $a + b = 180^{\circ}$ because they are
opposite angles in a cyclic quadrilateral. Substituting in the
expressions for $a$ and $b$ gives us $$d + f + h + j =
180^{\circ}$$
So $$(d + h) = 180^{\circ} - (f + j)$$
Looking back at the original diagram we can see that $(d + h)$
and $(f +j)$ are opposite angles in the quadrilateral and because
$(d + h) = 180^{\circ} - (f + j)$ the quadrilateral must be
cyclic.
Teachers' Resources
Why do this problem?
First, the surprising amount of variation in possibilities shown in the video is worth the journey. Secondly, even though there is such variation the outer quadrilateral is always cyclic.Finally, specialising by trying numbers can help form a map of the journey you need to make in order to prove the generalisation for any cyclic quadrilaterals.Possible approach
The first stage is simply to investigate:Construct an image with the given constraints either using dynamic geometry or with a ruler and compasses. Using ruler and compasses is difficult simply because you need some flexibility to ensure a reasonable overlap of the circles.
Are learners surprised by the flexibility visible in the dynamic image?
Allow time for lots of discussion about construction techniques, the order of working (formed by the constraints) and the freedoms available (how many circles will meet the cirteria?).
Now for the problem.
A first step is to encourage exploration by writing in some angle sizes (following a discussion of the properties of opposite angles of a cyclic quadrilateral). Does the outside quadrilateral have opposite angles whose sum is 180 degrees and is therefore cyclic?
In specialising by using numbers for angles and keeping track of which angles can be calculated from others, the steps to a generalisation are much clearer.
Key questions
- What defines a cyclic quadrilateral?
- What are the freedoms?
- What the contraints?
Possible support
Focus on the construction and looking at specific examples.For work on cyclic quadrilaterals try Pegboard Quads.
