Always the Same
Problem
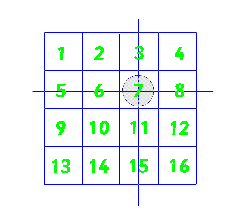
Arrange the numbers 1 to 16 into a 4 by 4 array.
Image
|
Choose a number and circle it. Cross out the
numbers which are in the same row and column as your chosen number.
Repeat this process twice more choosing from the remaining numbers. This should leave you with one number remaining, circle this one also. |
Image

|
Add up your four circled numbers.
Why do they always add up to 34 whatever way you choose your numbers? |
Student Solutions
Thank you to Jimmy, Natalie and Lucy at West Flegg GM Middle School for their work on the problem "Always the Same". Natalie is not the first student to add together all the numbers 1 through 16 and take the average.
Thus replacing the ascending numbers with 8.5 in every cell and circling four cells gives a total of 34. Or as Natalie did, she realised that "you pick numbers from each column and row" and took the average between the sum of the four columns:
i.e. (28 + 32 + 36 + 40)/4 = 34
A good solution with this method came from Melanie and Rachel of Flegg High School.
A proof of this problem could be as follows.
Let the first number be a.
Image

|
Then when choosing numbers from rows and column that do not
coincide we have: |
Hence:
4a + (4 + 8 + 12) + ( 1 + 2 + 3) = 34
i.e. 4a + 30 = 34
i.e a = 1
and the array is 1 through 16 as set.
But suppose the 'magic number' had been 62 then
4a + 30 = 62
i.e a = 8
and the array would have been 8 through 23.
Hope that the explanation above helps especially Josh at Russell Lower School to "work out where we went wrong".
We could have used a 5 by 5 array of ascending numbers!
