Two trees
Can you find the distance between the two trees using the information given?
Problem
Two trees, 20 metres and 30 metres long, lean across a passageway between two vertical walls.
They cross at a point 8 metres above the ground.
What is the distance between the foot of the trees?
Getting Started
Try thinking about similar triangles.
Student Solutions
You can solve this problem in many ways. One way involves using similar triangles, leading to a quartic equation which has to be solved by numerical methods. Sue Liu of Madras College used similar triangles and then the Newton Raphson to give a numerical solution
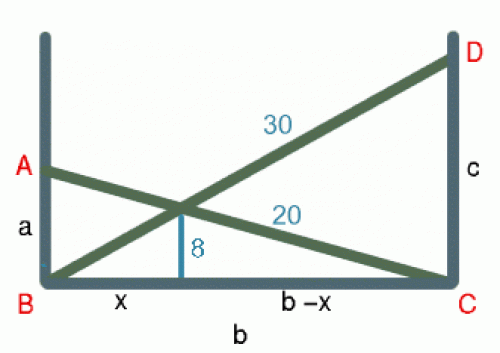
Let $AB = a$, $BC = b$, $CD = c$, $AC = 20$, BD = 30$, EF = 8$. By similar triangles:$${x \over b}= {8\over c}, \quad {b - x\over b} = {8 \over a}.$$ Adding these two expressions: $${8\over a} + {8\over c} = 1.\quad (1)$$ We can write $c$ in terms of $a$ using Pythagoras Theorem which gives: $$b^2 = 900 - c^2 = 400 - a^2. \quad (2)$$ and hence $$c^2 = 500 + a^2.$$ So (1) becomes $${8\over a} + {8\over \sqrt (500 + a^2)} = 1 \quad (3)$$ and we have to solve equation (3) to find $a$ and then we can find $b$ from equation (2). Rearranging (3) and squaring we get $${64\over (a^2 + 500)} = {(a - 8)^2\over a^2}.$$ Rearranging this equation gives: $$a^4 - 16a^3 + 500a^2 - 8000a + 32000 = 0.$$ Using the Newton Raphson method, or alternatively 'interval halving' gives the solution: $a = 11.712$ because the other roots of the quartic equation are less than 8 or complex. From this we get $b=16.212$ and $c=25.242$ so the distance between the bases of the trees is 16.212 metres (to 3 decimal places). Another approach is to set up a spreadsheet to give the height of the intersection of the ladders $h$ in terms of the distance $b$ between the trees at ground level using the equivalent of equation (1), namely: $${1\over \sqrt(400 - b^2)} + {1\over \sqrt (900 - b^2)} = {1\over h}.$$ Use the spreadsheet calculation, and interpolation, until $h = 8$ as nearly as required. This method will then give the corresponding value of $b$.
Teachers' Resources
Why do this problem?
It calls for constructing your own equation from the information given and then solving it by a numerical method (e.g. interval halving or the Newton Raphson method.)
Key question
When solving an equation $f(a) = 0$ can we find values of $a$ for which the function is positive and values for which the function is negative?
