Just Rolling Round
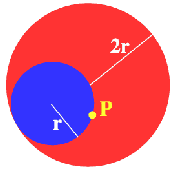
P is a point on the circumference of a circle radius r which rolls,
without slipping, inside a circle of radius 2r. What is the locus
of P?
Problem
Created with GeoGebra |
The smaller circle, radius $r$, rolls around without slipping inside the circumference of the larger circle, radius $2r$.
$P$ is a point on the circumference of the smaller circle . What is the locus of $P$? |
NOTES AND BACKGROUND
This dynamic image is drawn using Geogebra, free software and very easy to use. You can download your own copy of Geogebra from http://www.geogebra.org.
Getting Started
Experiment with the interactivity and make your own conjecture about the locus of $P$.
As the small circle moves, points on the small circle come into contact with points on the big circle. Think about the lengths of the arcs on the two circles that are made up of the points that have come into contact.
Student Solutions
|
Tomas of Malmsbury School, Mark of The
British School of Manilla and Herbert of Sha Tin College, Hong Kong
sent good solutions to this problem. Well done all of
you.
$P$ is a point on the circumference of a circle radius $r$
which touches another circle radius $2r$ on the inside. The smaller
circle rolls, without slipping, around the inner circumference of
the larger circle.
The point $P$ is a fixed point on the smaller circle which
moves as the small circle moves. The point $P_o$ is the position of
$P$ when $P$ is at the point of contact between the two circles.
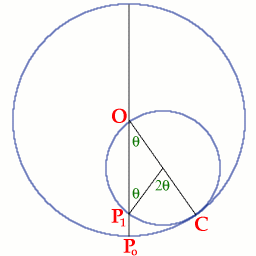
Consider the general position where the point of contact is the
point $C$ but here we do not assume that $P_1$ is the position of
the point $P$.
Image
|
By showing that the lengths of the arcs $P_oC$ and $P_1C$ are
equal, we shall prove that $P_1$ must be the position of the point
$P$ when the point of contact is at $C$. Hence we shall show that
$P$ must always lie on the diameter of the large circle through
$OP_o$.
Let $M$ be the centre of the small circle, then $MO = MP_1 =
MC = r$ and the triangle $OMP_1$ is isosceles. Hence $$\angle MOP_1
= \angle MP_1O = \theta$$ $$\angle P_1MC = \pi - (\pi - 2\theta) =
2\theta.$$ Hence, using the formula "arc length = radius x angle at
the centre of the circle": $$P_0C = (2r)(\theta) = 2r\theta$$ and
$$P_1C = (r)(2\theta) = 2r\theta.$$ Hence $P$ must be at the point
$P_1$ because the circle rolls without slipping, which shows that
the locus of P is the diameter of the larger circle.
Teachers' Resources
Image
|
Why do this problem?
In this
problem , the interactivity enables learners to experiment and
make their own conjectures about the locus. The proof requires only
simple geometrical reasoning involving circle theorems and arc
lengths.
Possible approach
Learners might first experiment with the interactivity and
make a conjecture about the locus, then try to prove their
conjecture.
|
Key question
We know the small circle rolls around inside the big one. What can we say about arc lengths?
Possible support
Learners might draw their own interactive diagrams using Geogebra.
Ask about how far a bicycle goes forward when the wheels rotate through exactly one revolution.
What about a revolution by a given angle?
What if the road was curved?
Possible extension
See the problem Illusion.
