Calcunos
Problem
Some time ago I was walking past a garage. Down on the ground was the big sign that they have that tells motorists how much the petrol will cost. You've probably seen them yourselves and you may have been asked to look out for the cheapest petrol around. The signs usually tell you the price for the different kinds of petrol. Since we measure in litres it's the price for one litre.
Well, this sign was being prepared to be put up by the side of the garage. I went over and looked at the part that shows the price. I was interested in how the numbers were shown and how they altered when the price changed. This particular one, like so many, showed the numbers like they are on a calculator display.
The little lines on a calculator display can be called 'light bars'. This is how they generally look for the figures 0 through to 9:-
In this sign they were brightly coloured flaps which on one side showed the colour and on the other side were blank. As I walked away from the garage I got thinking. This is the challenge that came to my mind.
If we had 16 light bars we could only make certain numbers. For example:-
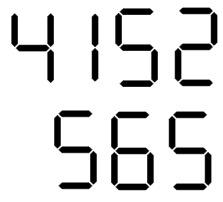
So, my challenge to you is to find all the numbers you can make, using 16 light bars all the time and forming the figures in the same way as I did them for 0 to 9.
When you've done a few you may be able to think of a method or system for helping you along the way. When you do, do write and let us know what it was, as well as sending us your solutions.
The last word, as usual, is to say when you are happy with what you have got, "I wonder what would happen if ...?''
Getting Started
How will you record what you've done?
How will you know when you have got all the possibilities?
Student Solutions
Here is a solution to Calcunos from Ned who has just left Christ Church Cathedral School in Oxford and is about to go to Abingdon School. Adam of Swavesey Village College, Cambridgeshire also sent in some good work on this investigation.
Dear Bernard
I have solved your question from the July challenges, CalcuNos, as there being 1,374 methods. The numbers of lightbars for each digit are:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 2 | 5 | 5 | 4 | 5 | 6 | 3 | 7 | 6 | 6 |
So we only need to consider combinations which add up to 16 using the numbers 2 to 7 and no others.
There are 32 ways of making 16.
| 7,7,2 | 6,6,2,2 | 5,5,4,2 | 4,4,3,3,2 |
| 7,6,3 | 6,5,5 | 5,5,3,3 | 4,4,2,2,2,2 |
| 7,5,4 | 6,5,3,2 | 5,5,2,2,2 | 4,3,3,3,3 |
| 7,5,2,2 | 6,4,4,2 | 5,4,4,3 | 4,3,3,2,2,2 |
| 7,4,3,2 | 6,4,3,3 | 5,4,3,2,2 | 4,2,2,2,2,2,2 |
| 7,3,3,3 | 6,4,2,2,2 | 5,3,2,2,2,2 | 3,3,3,3,2,2 |
| 7,3,2,2,2 | 6,3,3,2,2 | 4,4,4,4 | 3,3,2,2,2,2,2 |
| 6,6,4 | 6,2,2,2,2,2 | 4,4,4,2,2 | 2,2,2,2,2,2,2,2 |
The number of lightbars is unique except for three numbers which have 5 bars and three which have 6, so it is necessary to work out the number of different ways of arranging each set of numbers and then multiply by three for each of the 5's or 6's involved in the set.
For example:
7, 6, 3: the 3 could go in one of 3 places, the 7 in one of 2 (one has been taken up by the 3) and the 6 in one of 1; this makes 6 combinations.
| 7,6,3 | 7,3,6 | 6,7,3 | 6,3,7 | 3,7,6 | 3,6,7 |
However, as the 6 can represent any one of three numbers, one must multiply by 3, making a total of 18 combinations for numbers whose digits contain 7, 6 and 3 lightbars.
For combinations like 6,2,2,2,2,2 one sees that, as the 2's must be all the same, only 6 combinations exist (622222, 262222, 226222, 222622, 222262, 222226) times three (for the six), making 18 for this example.
The numbers of combinations for each set of numbers are:
| 7,7,2 | 3 |
| 7,6,3 | 18 |
| 7,5,4 | 18 |
| 7,5,2,2 | 36 |
| 7,4,3,2 | 24 |
| 7,3,3,3 | 4 |
| 7,3,2,2,2 | 20 |
| 6,6,4 | 27 |
| 6,6,2,2 | 36 |
| 6,5,5 | 81 |
| 6,5,3,2 | 216 |
| 6,4,4,2 | 36 |
| 6,4,3,3 | 36 |
| 6,4,2,2,2 | 60 |
| 6,3,3,2,2 | 90 |
| 6,2,2,2,2,2 | 18 |
| 5,5,4,2 | 54 |
| 5,5,3,3 | 36 |
| 5,5,2,2,2 | 90 |
| 5,4,4,3 | 36 |
| 5,4,3,2,2 | 180 |
| 5,3,2,2,2,2 | 90 |
| 4,4,4,4 | 1 |
| 4,4,4,2,2 | 10 |
| 4,4,3,3,2 | 30 |
| 4,4,2,2,2,2 | 15 |
| 4,3,3,3,3 | 5 |
| 4,3,3,2,2,2 | 60 |
| 4,2,2,2,2,2,2 | 7 |
| 3,3,3,3,2,2 | 15 |
| 3,3,2,2,2,2,2 | 21 |
| 2,2,2,2,2,2,2,2 | 1 |
This gives a grand total of 1,374 numbers which, on a calculator, have 16 light bars.
Teachers' Resources
Calcunos
Some time ago I was walking past a garage. Down on the ground was the big sign that they have that tells motorists how much the petrol will cost. You've probably seen them yourselves and you may have been asked to look out for the cheapest petrol around. The signs usually tell you the price for the different kinds of petrol. Since we measure in litres it's the price for one litre.
Well, this sign was being prepared to be put up by the side of the garage. I went over and looked at the part that shows the price. I was interested in how the numbers were shown and how they altered when the price changed. This particular one, like so many, showed the numbers like they are on a calculator display.
The little lines on a calculator display can be called 'light bars'. This is how they generally look for the figures 0 through to 9:-
In this sign they were brightly coloured flaps which on one side showed the colour and on the other side were blank. As I walked away from the garage I got thinking. This is the challenge that came to my mind.
If we had 16 light bars we could only make certain numbers. For example:-
So, my challenge to you is to find all the numbers you can make, using 16 light bars all the time and forming the figures in the same way as I did them for 0 to 9.
When you've done a few you may be able to think of a method or system for helping you along the way. When you do, do write and let us know what it was, as well as sending us your solutions.
The last word, as usual, is to say when you are happy with what you have got, "I wonder what would happen if ...?''