Up and Down Staircases
Always, Sometimes or Never? Shape
Method in multiplying madness?
Ice Cream
Always, Sometimes or Never? Number
Are these statements always true, sometimes true or never true?
Problem
Always, Sometimes or Never? Number statement cards
Are the following statements always true, sometimes true or never true?
How do you know?
Can you find examples or counter-examples for each one?
For the 'sometimes' cards can you explain when they are true? Or rewrite them so that they are always true or never true?
|
The sum of three numbers is odd |
If you add 1 to an odd number you get an even number |
|
Multiples of 5 end in a 5 |
If you add two odd numbers you get an odd number |
|
If you add a multiple of 10 to a multiple of 5 the answer is a multiple of 5 |
|
What about these more complex statements?
|
When you multiply two numbers you will always get a bigger number |
If you add a number to 5 your answer will be bigger than 5 |
|
A square number has an even number of factors |
The sum of three consecutive numbers is divisible by 3 |
|
Dividing a whole number by a half makes it twice as big |
|
You could print off and cut out the statement cards from the top of this page and arrange them in this grid.
Alternatively, you may like to try out your ideas using the interactivities below:
Getting Started
Can you think of an example when it isn't true?
How do you know that it is always true?
Is it possible to check all examples? Is there another way of knowing?
Student Solutions
We had some excellent solutions sent in for this task. Thank you to everybody who shared their ideas.
James from Hamstel Junior School in England made a chart of his answers, explaining his reasoning under each statement. You can click on the picture below to enlarge it.
Well done, James! James has used negative numbers to show that some of these statements aren't always true.
Trisan, Rudy and Marcos from Sahauro in the USA used zero to show that some of the statements aren't always true:
If you multiply 2 numbers you can't always get a bigger answer because you can do zero times five and it will be zero.
Well done for thinking carefully about how to disprove some of these statements, even if they do always work for positive whole numbers.
Prayaan from King's College Junior School in the UK gave clear explanations for his thoughts about each statement, particularly for why a square number must have an odd number of factors:
Each factor usually has a ‘partner’ to multiply to form the original number, so there will be an even number of factors. But for square numbers, the square root doesn’t have a ‘partner’ because it multiplies itself to form a square number. So square numbers never have even number of factors.
Thank you for sending in your explanations, Prayaan. Have a look at Prayaan's full solution and see if you agree with all of his explanations. Most of the solutions we received said that dividing a whole number by a half does always make it twice as big - however, Prayaan thinks that this might not always be true:
This is true for numbers greater than 1, but for negatives, the number becomes smaller. -3 ÷ 0.5= -6
This is a really interesting way of thinking about it, Prayaan. I wonder if -6 is 'twice as big' as -3, or if we can't use that phrase because it would be below -3 on a number line. If you have any ideas about this, please email us.
Teachers' Resources
Why do this problem?
These tasks are a great opportunity for learners to use reasoning to decipher mathematical statements. We often make mathematical claims that are only true in certain contexts and it is important for learners to be able to look critically at statements and understand in what situations they apply.
The examples here only refer to one key topic but similar statements could be created for any area of maths - we have made some similar problems about shape.
Possible approach
You may want to start with one statement and have a class discussion about whether it is true. Ask learners to think of some examples to illustrate the statement and decide whether it is always, sometimes or never true. If they decide it is sometimes true, they could think about what conditions make it true.
Groups of learners could be given the set of statement cards to sort into the grid sheet, or they could use the interactivities on a tablet/computer. Taking each card in turn they could decide if it is always, sometimes or never true. Then they could justify their reasoning. If they think it is always true or never true, they could explain why they think this is. If they think it is sometimes true they could start by coming up with cases for each and trying to generalise.
For learners who have had more experience of reasoning it might be good to ask them to try and write their ideas down in a clear way, perhaps for just one or two of the statements to start with.
It would be worth sharing ideas as a class at the end. You could pick up on a statement that has been problematic or where there does not seem to be a consensus and support a whole class discussion.
Key questions
Can you think of an example when it isn't true?
How do you know that it is always true?
Is it possible to check all examples? Are there other ways of knowing?
Possible support
When discussing as a class, suggest types of numbers to consider. Learners often need to start with concrete examples to develop their understanding of a particular concept before they can develop their reasoning within that area. Concrete resources can be useful for developing an understanding of the structure of numbers, and can be used by all learners to support their arguments.
The similar problems Always, Sometimes or Never? KS1 and Always, Sometimes or Never? might be a good starting point for pupils who need more support.
Possible extension
Learners could be asked to come up with their own statements that are always, sometimes and never true within a topic area. Again they should try to justify their reasons and specify the conditions necessary.
Sets of Numbers
Problem
How many different sets of numbers with at least four members can you find in the numbers in this box?
For example, one set could be multiples of $4$ {$8, 36 ...$}, another could be odd numbers {$3, 13 ...$}.
Getting Started
You could list all the properties of each number as a start.
Can you see some numbers which have the same property?
Student Solutions
Children from Beaumaris North Primary School, Melbourne told us:
In our Year 3 Enrichment group we discussed all the possible sets that could be found. Here is what we found!even numbers {$2, 8, 36, 56, 64, 136$}
odd numbers {$3, 13, 17, 27, 39, 49, 51, 91, 119, 121, 125, 143$}
multiples of one {all of them!}
multiples of $2$ {$2, 8, 36, 56, 64, 136$ - the same as even numbers!!}
multiples of $3$ {$3, 27, 36, 39, 51$}
multiples of $4$ {$8, 36, 56, 64, 136$}
multiples of $7$ {$49, 56, 91, 119$}
multiples of $8$ {$8, 56, 64, 136$}
numbers starting with $1$ {$13, 17, 119, 121, 125, 136, 143$}
square numbers {$36, 49, 64, 121$}
numbers containing $2$ {$2, 27, 121, 125$}
square roots {all of them are square roots !}
numbers containing $1$ {$13, 17, 51, 91, 119, 121, 125, 136, 143$}
numbers containing $6$ {$36, 56, 64, 136$}
cube numbers {$8, 27, 64, 125$}
numbers containing $3$ {$3, 13, 36, 39, 136, 143$}
prime numbers {$2, 3, 13, 17$}
numbers containing $9$ {$39, 49, 91, 119$}
numbers that you can subtract one from {all of them again!}
numbers between one and one hundred and forty four {all of them AGAIN!}
numbers between one and one hundred {$2, 8, 13, 17, 27, 36, 39, 49, 51, 56, 64, 91$}
whole numbers {all of them}
triple digit numbers {$119, 121, 125, 136, 143$}
numbers with double digits {$13, 17, 27, 36, 39, 49, 51, 56, 64, 91$}
We enjoyed this because we liked picking out different possibilities and seeing if they worked out. We could have submitted more but the bell rang! Thanks for the great challenge.
Olly from North Molton Primary also found:
multiples of $13$: {$13, 39, 91, 143$}multiples of $17$: {$17, 51, 119, 136$}
... and multiples of $1$ which of course is all of the numbers.
Jin and Anushkawho go to Dubai International Academy had one more set:
digits add to $8${$8,17,125,143$}
Can you find any more? How about triangle numbers and tetrahedral numbers?
Teachers' Resources
Sets of Numbers
How many different sets of numbers with at least four members can you find in the numbers in this box?
For example, one set could be multiples of $4$ {$8, 36 ...$}, another could be odd numbers {$3, 13 ...$}.
Why do this problem?
This problem gives plenty of opportunity for both discussion and exploring patterns, properties and relationships involving numbers. It also helps learners to make general statements about properties of numbers such as squares, factors, multiples, odd and even, and to identify examples for which a statement is true or false.Possible approach
Key questions
Possible extension
Learners could make their own list of numbers to make into as many sets as possible. You could suggest using triangular and cube numbers as well as various multiples.Possible support
Some children might find it useful to list all the properties of each number in the box.Baravelle
What can you see? What do you notice? What questions can you ask?
Problem
Look at this image for a short while before turning away.
Can you:
- Recreate the image?
- Describe the image?
- Say some mathematical things about what you notice?
- Think of some mathematical questions you would like to ask about it?
You can download a PDF of the image to look at.
Teachers' Resources
Baravelle
Look at this image for a short while before turning away.
Can you:
- Recreate the image?
- Describe the image?
- Say some mathematical things about what you notice?
- Think of some mathematical questions you would like to ask about it?
You can download a PDF of the image to look at.
Why do this problem
The aim of using this image is to encourage discussion about the different ways of seeing, and to pose questions that can form the focus of further investigation.
Possible approach
You can find a pdf with the image here. Look at the image for about a minute and then "hide it". Then share ideas.
Follow up by selecting one or two of the ideas for the group to explore further, for example:
- Recreating the image
- Finding what fraction of the whole the areas is shaded red, blue and white.
Key questions
Can you continue the pattern inwards? Outwards?
Can you give a convincing argument for the fractions of the whole that you can see?
Possible Extension
Consider summing infinite series.
What are the ratios of the lengths of the sides of the triangles?
Possible support
Can you find the fractions and or recreate the shape by folding? Some learners might like to try the problem Inside Seven Squares.
Tiles on a Size Ten Patio
Problem
Imagine that round the back of where you live is a piece of ground that your family want to change. Instead of grass or plants growing there you want to have a patio. To prepare to change it the ground is dug up and levelled, it is then measured and found to be a square $10$ by $10$ [this could be feet, metres or yards it does not really matter for this challenge]. You then go to a large store that sells tiles to go on the ground. To your surprise you find that they sell tiles in ten different sizes; $1$ by $1$, $2$ by $2$, $3$ by $3$, etc. up to $10$ by $10$. You decide to go back home for a while and work a few ideas out.
You start by drawing a $10$ by $10$ square; and then you think about what sizes of tiles to use to cover it.
If you use $1$ by $1$ tiles then you find [or know already!] that you will need $100$ of them. So your shopping list would look like :-
$100$ tiles @ $1$ by $1$ > Total number of tiles $100$
If you use $10$ by $10$ tiles then you find [or know already!] that you will need 1 of them. So your shopping list would look like :-
$1$ tiles @ $10$ by $10$ > Total number of tiles $1$
If you use $2$ by $2$ tiles then you find [or know already!] that you will need $25$ of them. So your shopping list would look like :-
$25$ tiles @ $2$ by $2$ > Total number of tiles $25$
You could of course use a mixture of different sized tiles.
If you use $12$ tiles $2$ by $2$ and $4$ tiles $3$ by $3$ and $1$ tile $4$ by $4$ your shopping list would look like :-
$12$ tiles @ $2$ by $2$
$4$ tiles @ $3$ by $3$
$1$ tile @ $4$ by $4$ > Total number of tiles $17$
So you could, with these examples use $1, 17, 25$ or indeed $100$ tiles.
Your challenge starts by asking you to try to find lots of different numbers of tiles that could be used to cover this $10$ by $10$ patio.
You could think about the artistic appearance of it as well if you like. However all the patio must be covered and no cutting any of them to make different sizes or shapes ... they're actually very, very hard to cut anyway.
You could now think about these kinds of questions and perhaps you would think of other questions of your own to pursue.
- Are there some numbers of tiles used that actually are made up of different mixtures of tiles? [For example in our one that used $17$, could you get to use just $17$ tiles but they require a different shopping list from the one above?]
- Are there some numbers between $1$ and $100$ that cannot be used as the total number of tiles required?
- Is there some system for getting new examples that use different numbers of tiles?
Getting Started
Using squared paper and drawing your arrangement of tiles might help.
Can you use one of the ways you've already found to find a way using a different number of tiles? Try changing just a part of it, perhaps.
Student Solutions
These solutions are just some examples showing the work of four children.
First of all we have Izzy's examples:-
Image
|
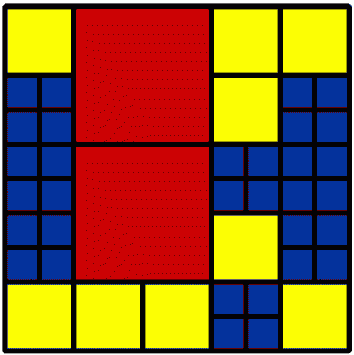
9 2 by 2 2 4 by 4 32 1 by 1 43 Total |
Image
|
96 1 by 1 1 2 by 2 97 Total |
Izzy found that you could not get a solution using 98 or 99 tiles so the next highest after 100 was this one with just 1 2 by 2 replacing 4 1 by 1's.
Now we see Lizzy's:-
Image
|
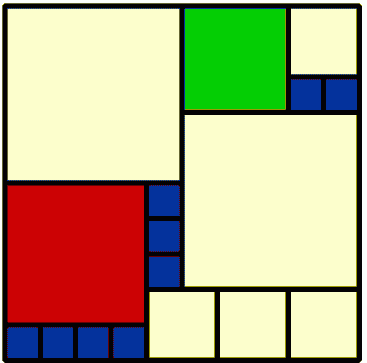
2 5 by 5 1 3 by 3 1 4 by 4 4 2 by 2 9 1 by 1 17 Total |
Image
|
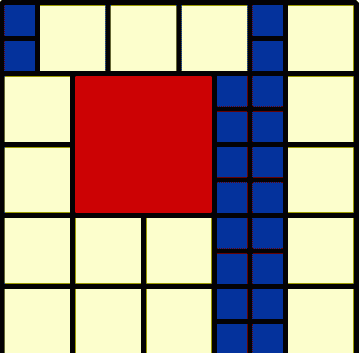
16 2 by 2 20 1 by 1 1 4 by 4 37 Total |
I rather liked her 17 made up of 5 different sizes. The 37 was not symmetrical, many results were, that's neither good nor bad ... it's all O.K.
Then we have Ben:-
Image
|
20 2 by 2 20 1 by 1 40 Total |
Image
|
8 2 by 2 1 6 by 6 32 1 by 1 41 Total |
His 41 would really look good if you wanted it to be very symmetrical. You could probably invent some games in going around the edge from 4 1 by 1's to a 2 by 2. The 40 is interesting because there is the same number of each tile size.
Image
|
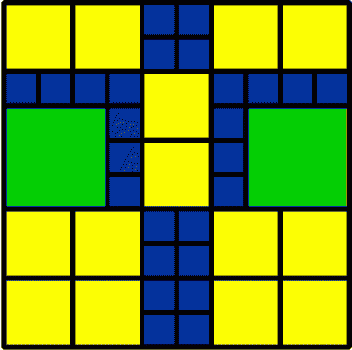
14 2 by 2 2 3 by 3 26 1 by 1 42 Total |
Image
|
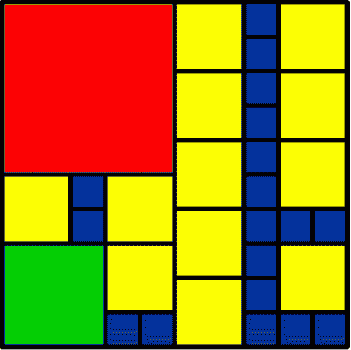
12 2 by 2 1 3 by 3 1 5 by 5 18 1 by 1 32 Total |
I think Bo's 42 is rather like a robot! The 32 was very different.
Well done and thank you Izzy, Lizzy, Ben and Bo. Yes these are four real children from the South West of England who were in a group of 19 doing this activity.
Teachers' Resources
Tiles on a Patio
Imagine that round the back of where you live is a piece of ground that your family want to change. Instead of grass or plants growing there you want to have a patio. To prepare to change it the ground is dug up and levelled, it is then measured and found to be a square $10$ by $10$ [this could be feet, metres or yards it does not really matter for this challenge]. You then go to a large store that sells tiles to go on the ground. To your surprise you find that they sell tiles in ten different sizes; $1$ by $1$, $2$ by $2$, $3$ by $3$, etc. up to $10$ by $10$. You decide to go back home for a while and work a few ideas out.
You start by drawing a $10$ by $10$ square; and then you think about what sizes of tiles to use to cover it.
If you use $1$ by $1$ tiles then you find [or know already!] that you will need $100$ of them. So your shopping list would look like :-
$100$ tiles @ $1$ by $1$ > Total number of tiles $100$
If you use $10$ by $10$ tiles then you find [or know already!] that you will need 1 of them. So your shopping list would look like :-
$1$ tiles @ $10$ by $10$ > Total number of tiles $1$
If you use $2$ by $2$ tiles then you find [or know already!] that you will need $25$ of them. So your shopping list would look like :-
$25$ tiles @ $2$ by $2$ > Total number of tiles $25$
You could of course use a mixture of different sized tiles.
If you use $12$ tiles $2$ by $2$ and $4$ tiles $3$ by $3$ and $1$ tile $4$ by $4$ your shopping list would look like :-
$12$ tiles @ $2$ by $2$
$4$ tiles @ $3$ by $3$
$1$ tile @ $4$ by $4$ > Total number of tiles $17$
So you could, with these examples use $1, 17, 25$ or indeed $100$ tiles.
Your challenge starts by asking you to try to find lots of different numbers of tiles that could be used to cover this $10$ by $10$ patio.
You could think about the artistic appearance of it as well if you like. However all the patio must be covered and no cutting any of them to make different sizes or shapes ... they're actually very, very hard to cut anyway.
You could now think about these kinds of questions and perhaps you would think of other questions of your own to pursue.
- Are there some numbers of tiles used that actually are made up of different mixtures of tiles? [For example in our one that used $17$, could you get to use just $17$ tiles but they require a different shopping list from the one above?]
- Are there some numbers between $1$ and $100$ that cannot be used as the total number of tiles required?
- Is there some system for getting new examples that use different numbers of tiles?
You might then think about how all this might or might not change if the patio had been $9$ by $9$ [$8$ by $8$, $7$ by $7$ etc ...]
Well good luck, and if you're artistically inclined I guess that you may have some results that would look really good displayed. Since you're sitting at a computer it may be that you could use a "draw/art" package to do all the work on the screen for you. But have a break from the screen every hour ... your body deserves it!
Why do this problem?
Possible approach
Key questions
Possible extension
For the exceptionally mathematically able
These pupils could work towards comparing results with different sized patios and making statements about those arrangements that use the same number of tiles but different tiles. They could then look at My New Patio and before working on it, predict what the similarities and differences will be in the solutions of both activities.
Possible support
polygonals
Problem
Polygonal numbers are those that are arranged in shapes as they enlarge (starting with $1$). Here are examples of the $5$th polygonal numbers for the first $7$ shapes Triangle ($3$) through to Nonegon ($9$).
and for example, the centred hexagon numbers go $1, 7, 19, 37, 61$.
Now it's over to you!
This investigation invites you to explore these sets of numbers and explore relationships within ordinary polygonal numbers and/or centred polygonal numbers.
You could also explore relationships between ordinary polygonal numbers and the centred polygonal numbers.
For example, you could explore which different polygonals (both centred and ordinary) have the same number occuring in the series?
KEY QUESTIONS:
What is the relationship between ordinary triangular polygonal numbers and others?
Can you re-arrange the dots from one polygonal to make another, and then generalise?
Throughout your exploration the question "Why?" probably needs to be asked!
Getting Started
Teachers' Resources
Polygonals
Polygonal numbers are those that are arranged in shapes as they enlarge (starting with $1$). Here are examples of the $5$th polygonal numbers for the first $7$ shapes Triangle ($3$) through to Nonegon ($9$).
and for example, the centred hexagon numbers go $1, 7, 19, 37, 61$.
Now it's over to you!
This investigation invites you to explore these sets of numbers and explore relationships within ordinary polygonal numbers and/or centred polygonal numbers.
You could also explore relationships between ordinary polygonal numbers and the centred polygonal numbers.
For example, you could explore which different polygonals (both centred and ordinary) have the same number occuring in the series?
KEY QUESTIONS:
What is the relationship between ordinary triangular polygonal numbers and others?
Can you re-arrange the dots from one polygonal to make another, and then generalise.?
Throughout your exploration the question "Why?" probably needs to be asked!
Why do this problem?
Possible approach
Key questions
Possible extension