Teaching Fractions With Understanding: Part-Whole Concept
In her studies of children learning about rational numbers, Grace Lopez-Charles [see Note 1 below] has identified some different perspectives through which children see fractions. This article starts looking at some of those perspectives, firstly by considering what happens in situations where learners are trying to create equal shares. From sharing using halves learners move to partitioning using other divisions, such as fifths or sixths. This results in the need to develop understandings of equivalence which is discussed in the second section of this article. Finally, we look at some ways of teaching fractions more effectively that arise from Grace's work.
Equal shares
Working with halves
Stuck on counting
Partitioning
Even young children can partition regions or composite units approximately equally among two or three recipients. The older, more mathematically-mature child can partition the region into $x$ number of parts and then designate $y$ of the parts to indicate $\frac{y}{x}$ where $x$ is greater than $2$.For example: $8$ year-old children were asked to divide a rectangle into eight pieces and then colour two of the pieces red in a diagram similar to the one below.

In seeing the fraction as a partition and identifying what is the same and what is different about $\frac{3}{4}$ and $\frac{6}{8}$ learners begin to see the fraction as a comparison between the numerator and the denominator (what Grace calls one-to-many or many-to-many comparison). This is based on a ratio concept and Grace argues it also indicates a deeper understanding of fractions. As in the previous example, a child indicating that the uncoloured fraction of the square is three-quarters, is simplifying the denominator and numerator to give an equivalent fraction, without losing the value of the fraction, though some information is lost.
What impact might this have on how we teach children to understand fractions better?
Ideas for teaching fractions
When teaching fractions in schools, the emphasis is often on situations where the object can easily be cut, folded, split or coloured in equal parts. Although there is some need for this sort of activity, children should be exposed to a wide variety of situations, some where such folding or splitting strategies will not be successful. In experiencing a variety of situations where fractions can be found, learners will have the opportunity to reflect and abstract critical relations in different contextual situations. In other words, children must see a whole in all its representational forms. This will aid them in developing a more robust grasp of the concept of a fraction. Grace describes some of these situations in terms of properties of being discrete or continuous, definite or indefinite (see below). Thus the aim is to engage in working in situations that offer opportunities to explore fractions in each of these situations.
- Show the children some sweets; question them:- Do you think I have enough sweets that each child will get one sweet?; What will happen if I cut each sweet in half?; Will more or less children get sweets?
- Encourage the children to make meaningful comparisons e.g. '3 pizzas, 4 children', 'does everyone get more or less than half of a pizza? Does everyone get more or less than a whole pizza?'
By presenting the problem qualitatively, teachers are able to generate useful discussions that will encourage the children to use, question and develop their own approaches.
The types of items a teacher sets for individual or group activities should be geared towards developing the fraction concept with the purpose of overcoming some of their difficulties with fractions. By presenting the children with wholes, which are not explicitly divided into equal parts, they are encouraged to analyse the part-whole relationship.
For example:
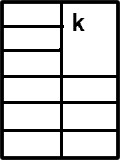
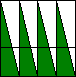
For each figure, write the fraction shown:
(a)What fraction is K?
(b)What fraction of the figure is not coloured?
(c)What fraction of the whole is missing?
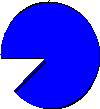
Where there is an explicit division of a whole into equal parts, children are able to determine the fraction of the part/parts indicated by counting the number of parts in the whole and the number of parts indicated (double counting). In the figures presented above, it is more difficult for the children to adopt this 'partitioning' approach. Children are required to analyse the relationship of the particular part/parts indicated in relation to the entire whole.
Fractions taught as a part-whole concept, in the manner indicated in this article, can ensure that children have a sound foundation for conceptualising other concepts in fractions. However, it must be noted that despite the wealth of possible examples, an approach to fractions based solely on "part-whole" is too restricted - yielding proper fractions only. Therefore other concepts of fractions need to be explored if children are to have a fuller and better understanding of rational numbers.
Note 1: This article is based on research by Grace Lopez-Charles - Assessment of Children's Understanding of Rational Numbers - PhD Thesis.
References:
- Azis, N & Pa, N (1991), Primary school pupils' knowledge of fractions, Journal for Research in Education, 45
- Nunes, T., (1996), Understanding rational numbers, in T. Nunes and P.E. Bryant (eds.): Children Doing Mathematics. Oxford: Blackwell Publishers.
- Streefland, L. (1996), Charming fractions or fractions being charmed? In T. Nunes and P.E. Bryant (eds.): How Do Children Learn Mathematics? Hove: Erlbaum.
