
Year 11+ Being resilient
-

-
 game
gameLast Biscuit
Can you find a strategy that ensures you get to take the last biscuit in this game?
-
 problemFavourite
problemFavouriteCrossing the Bridge
Four friends must cross a bridge. How can they all cross it in just 17 minutes?
-

-
 problemFavourite
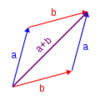
problemFavouriteVector Walk
Starting with two basic vector steps, which destinations can you reach on a vector walk?
-
 problemFavourite
problemFavouriteMega Quadratic Equations
What do you get when you raise a quadratic to the power of a quadratic?
-

-

-
 problemFavourite
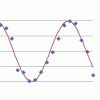
problemFavouriteBack Fitter
10 graphs of experimental data are given. Can you use a spreadsheet to find algebraic graphs which match them closely, and thus discover the formulae most likely to govern the underlying processes?
-
 problemFavourite
problemFavouriteKite in a Square
Can you make sense of the three methods to work out what fraction of the total area is shaded?
-
 problemFavourite
problemFavouriteSnooker Frames
It is believed that weaker snooker players have a better chance of winning matches over eleven frames (i.e. first to win 6 frames) than they do over fifteen frames. Is this true?
-
 problemFavourite
problemFavouriteAreas and Ratios
Do you have enough information to work out the area of the shaded quadrilateral?
-
 problemFavourite
problemFavouriteGiants
Which is the bigger, 9^10 or 10^9 ? Which is the bigger, 99^100 or 100^99 ?
-

-
 problem
problemCrazy Cannons
Two cannons are fired at one another and the cannonballs collide... what can you deduce?
-
 problem
problemFrosty the Snowman
Frosty the Snowman is melting. Can you use your knowledge of differential equations to find out how his volume changes as he shrinks?
-
 problem
problemThe Derren Brown coin flipping scam
Calculate probabilities associated with the Derren Brown coin scam in which he flipped 10 heads in a row.
-

