A Little Light Thinking
Here is a machine with four coloured lights. Can you make two lights switch on at once? Three lights? All four lights?
Problem
A Little Light Thinking printable worksheet
Can you figure out a method to make all four lights on the machine below switch on at once?
This problem follows on from Charlie's Delightful Machine, where you are invited to find strategies for working out the rules controlling each light.
The rules for turning on the lights are all given by linear sequences (like those found in Shifting Times Tables).
What is special about a rule where all the 'light on' numbers
- are odd?
- are even?
- are a mixture of odd and even?
- are all multiples of 3? Or 4? Or...
- have a last digit of 7?
Can you make two lights light up together?
Once you have made two lights light up together, can you find another number that will light them both up? And another? And another? ...
Can you find any connections between the rules that light up each individual light and the rule that lights up the pair?
What about trying to light up three lights at once? Or all four?
Sometimes it's impossible to switch a pair of lights on simultaneously.
How can you decide whether it is possible to switch a pair of lights on simultaneously?
Or a set of three lights? Or all four?
Getting Started
The problem Shifting Times Tables offers an introductory challenge for exploring linear sequences.
The problem Remainders explores some properties of numbers which could be useful when thinking about this problem.
Student Solutions
The solutions shown here do not include much information about how to find the rules which control each light. To see solutions on how to find the rules, have a look at Charlie's Delightful Machine.
Rishika from Nonsuch High School for Girls in the UK submitted a solution to the first part of the problem:
In arithmetic sequences, there is a number which is added or subtracted to obtain the next term - this is called the common difference and is shown by the coefficient of $n$ when [an expression for] the $n^\text{th}$ term is found.
For example, the sequence $1,3,5,7,\ldots$ has a common difference of $2$ and an $n^\text{th}$ term of $2n-1$.
$2(1)-1=1$
$2(2)-1=3$
$2(3)-1=5.$
The '$-1$' is the '$0^\text{th}$ term', is found by subtracting the common difference from the first term ($1-2$).
When all the 'light on' numbers are odd, the $n^\text{th}$ term rule always has to have an odd '$0^\text{th}$ term' and an even common difference.
The c.d has to be even because an odd common difference will generate a sequence with both even and odd terms (e.g. $3n = 3,6,9,\ldots$).
The '$0^\text{th}$ term' must be odd because if a sequence has an even c.d and $0^{th}$ term, it will always have even terms (e.g. $2n+2 = 4,6,8, \ldots$).
Some examples include:
$2n-1 = 1,3,5,7,\ldots$
$-6n-9 = -15,-21,-27,\ldots$
However, the common difference has to be an integer for this to hold true.
When all the 'light on' numbers are even, the $n^\text{th}$ term rule always has to have an even '$0^\text{th}$ term' and an even common difference.
Examples:
$2n-2 =0,2,4,6,\ldots$
$-6n-8 = -14,-20,-26,\ldots$
In sequences with a mixture of odd and even numbers, the $n^\text{th}$ term rule always has to have an odd common difference because an even common difference will result in a sequence with only odd or only even terms.
Some examples include:
$3n-2 =1,4,7,10,\ldots$
$-5n-8 = -13,-18,-23,\ldots.$
When the terms are all multiples of a number:
For example:
$3,6,9,12.,\ldots$ contains multiples of $3$ and has an $n^\text{th}$ term of $3n$.
$4,8,12,16,\ldots$ contains multiples of $4$ and has an $n^\text{th}$ term of $4n$.
$100,200,300,\ldots$contains multiples of $100$ and has an $n^\text{th}$ term of $100n$.
Also, there must either be no $0^\text{th}$ term, or a $0^\text{th}$ term which is also a multiple of the c.d of the sequence. This is proved by:
$3n-1$ (which does not work as $-1$ is not a multiple of $3$, which is the c.d) = $2,5,8,\ldots$
However, $3n-15 = -12,-9,-6,\ldots$ (as $-15$ is a multiple of $3$, which is the c.d).
A sequence which has a last digit of $7$ must have an $n^\text{th}$ term rule that has a common difference of a multiple of $10$ and then a $0^\text{th}$ term ending in either $-3$ or $+7$.
This is because a multiple of $10$ $+7$ or $-3$ will always result in an integer ending in $7$ (so the first term will end in $7$, and then, because you add on a multiple of $10$ each time, all of the other terms will also end in $7$). Examples include:
$10n-3 = 7,17,27,\ldots$
$100n+7= 107,207,307,\ldots$
Alternatively, if the multiple of $10$ as the c.d is negative, the $0^\text{th}$ term must be $+3$ or $-7$. Examples:
$-100n+3 = -97,-197,-297,\ldots$
$-10n-7= -17,-27,-37,\ldots$
Hondfa, Laurenc and Shafi from Greenacre Public School in Australia found some numbers that lit up more than one lightbulb for their rules:
Our rules we got for Level 1 were:
Blue: Every 6th number after three.
Red: The last digit of the number must be one.
Green: Every 9th number.
Yellow: Every 11th number after eight.
1) The number 9 lights up the blue and green bulb. A few other numbers that also light up the pair of light bulbs are; 27, 45, 63, 81 etc.
2) The rule for lighting up the bulbs - blue and green, is every 18th number after 9. We also found that Numbers 81 and 63 light up 3 bulbs, while the number 261 lights up all four light bulbs.
3) If you want to see if you can switch on a set of light bulbs instantly, you must find out the rule belonging to their light bulb. Once you've done that, find out if they match with each other, merge them together to create a new rule to figure the number to activate a pair, triad or a quartet of light bulbs.
Kevin from Harrow International School Hong Kong also found some numbers that lit up more than one bulb, and included a level 2 rule:
In order to find a number to light up as many bulbs as possible, you need to find the rule of the bulb first and see whether it's possible for another rule of another bulb to have a "matching point" with the rule of this bulb. For example, it shows the rules of the yellow bulb being the multiples of 3 and the red bulb being multiples of 5. Some multiples of 3 has the last digit either a 5 or a 0 which means it's a multiple of 5.
Therefore, it is possible for the yellow and red bulb to light up at the same time (the number 15 works for example).
From the rule of the green bulb, it can land on any digit, including 5 and 0 (Kevin's rule for the green bulb was "Goes up by 8, starting from 7"). So it is possible for three bulbs to light up at the same number, which is the yellow red and green bulbs (again, the number 15 works).
I decided to reload the bulbs with new rules following the method I used to find the rules of the bulbs. And these were the new rules of the bulbs I found:
Yellow: Goes up by 3, starting from 1
Red: Goes up by 12, starting from 6
Blue: Every even number's square
Green: Goes up by 6, starting from 4
The blue bulb was special and when the only numbers I found were 0, 4 and 16, I noticed they were all squares of the sequence of even numbers (that being 0, 2 and 4).
Since the yellow bulb can be lit up by an even square (e.g. $4, 16, 64, 100,\ldots$), the blue bulb can be lit up at the same time, and it's possible for two bulbs to light up at the same number. The green bulb can also be lit up by an even square, so it's possible for three bulbs to light up at the same number. With the red's rule, it's not possible for it to light up at a square number (or if it was, it would be really high, but it will take a long time to find it out), so only three bulbs can be lit up at the same time (I think).
It is true that no number which satisfies red's rule can be a square number. This is because all of the numbers in the sequence are even, but none of them are multiples of 4 (why? Use the last part of Rishika's solution). However, all even squares are the squares of even numbers (since odd$\times$odd is odd and even$\times$even is even), and the square of an even number is always a multiple of 4 (why? Think about the factors that all even numbers have, and what happens when you square them).
Vicente from King's College Alicante in Spain had a method for finding which numbers will light up more than one bulb:
Yellow: it is rising constantly by $7$ and that the first number is $2$ so you can say that the rule for lighting up yellow is $7n-5$
Red: it is rising constantly by $11$ and the first number being $9$ you would have to $-2$ therefore the rule is: $11n-2$
Blue: there is a constant increase of $10$, and $4$ being the starting point you will have to subtract $6$; making the rule for blue: $10n-6$
Green: there is a constant difference of $12$, and again being $6$ the starting point you are going to take off $6$. Making the rule for green: $12n-6$
In order to answer the next question it will be easier to put the equations like this, where $x$ is the number on the sequence lighting up.
Y: $ ( x + 5 ) / 7 = n$
R: $( x + 2 ) / 11 =n$
B: $( x + 6 ) / 10 = n$
G: $( x + 6 ) / 12 = n$
To check if two light bulbs will light up, the $x$ number will have to be the same, and after adding or subtracting the other number after $x$, it needs to be exactly divisible by the number it is divided, in both.
For example, if $x$ lights up the yellow and red bulbs, then $(x+5)$ is divisible by $7$ and $(x+2)$ is divisible by $11$.
But is there an easier way to check this? Yes there is, the number that you are adding on or subtracting after $x$ has to have a difference, to explain it better let's consider Y and R which are $5$ and $2$, the difference between them is $3$. Therefore you will need to find multiples of both denominators ($7$ and $11$) that differ from each other by $3$, (the difference of $3$ is relevant because $x+5=(x+2)+3$, so the multiple of $7$ (which is $(x+5)$) must be $3$ more than the multiple of $11$ (which is $(x+2)$)). So in this case it will be $14$ and $11$. To find $x$ then you will just have subtract $5$ from $14$ or subtract $2$ from $11$ to get the answer, which in this case is $9$.
In this case, it is possible to light up 3 bulbs when both blue and green bulbs are lit. This is because both, as explained before, [have $(x+6)$ as the numerator]. So for there to be three lit up bulbs there needs to be a multiple of $7$ which, to a common multiple of $10$ and $12$, differs by $1$. Another possible combination for there to be 3 light bulbs lit up is having a multiple of $11$ which, to a common multiple of $10$ and $12$, differs by $4$.
McKenna from ISL in Switzerland investigated what makes it impossible for several bulbs to light up simultaneously, using graphs and Excel.
The first step to solving this problem is to figure out the pattern. I did this by listing out the numbers that lit up starting at $0$. For the green light bulb I wrote out $0,10,20,30,\ldots$ It was clear that the pattern could be represented in a linear function; in this case the function would be $y = 10x$. Repeat this 3 more times to get the 4 other bulbs' functions. After I had the 4 equations I immediately thought to plot in in a graph as it would help me visualize the pattern and it looked something like this. The lights light up at the whole number intersections.
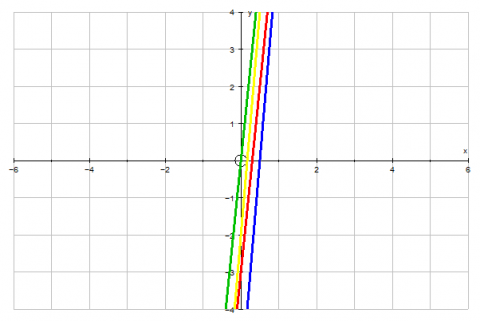
But this representation is problematic as it is unclear when the lights light up. It did shed some light (pun intended) on when lines cannot cross. In the graph above 2 lines (the green and the blue) have the same slope, but crossed the y axis at a different time so they were parallel.
It was hard to go any further with this representation as even though it express the green lights pattern as $y = 10x$ it could be expressed as $y = 10x - 10$, $y = 10x + 10,...$
This is because the rules such as $y=10x-10$, $y=10x-20$ would light up at exactly the same numbers as $y=10x$, but would look like different lines on the graph. So two bulbs would light up when a differently coloured line crossed any of the lines $y=10x-10$, $y=10x-20$ etc. And each bulb should also have a whole family of lines like this one - for example, the red bulb, as well as having the line $y=12x-6$, should also have $y=12x+6$, $y=12x+18$, etc.
So I used excel to make a table that looks like this...

Every white space is when the light is on and every black space is when the light is off. So when 2 spaces are white in the same row they light up together. This picture only goes to 20 rows. On the spreadsheet there are 386 rows.
From this table we can tell that blue and green will never light up together because they are parallel (as seen from the graph) this can also apply to the yellow light and the red light. (On the table you can see that the gaps between the white spaces are the same for the green and blue lights, and the gaps are also the same for the red and yellow lights, so in each case the pair can never light up together. This is what McKenna means by 'parallel', although parallel usually refers to lines like the ones on the graph).
From this table we can tell that the red and blue light will never light up together. I know this because the first positive integer for the red light is $6$ and the slope is $12$ and because anytime you add an even number to an even number you get an even number (even + even = even). So the red light can only light up at even numbers. The blue light can only light up on odd numbers because the first positive integer is $7$ and the slope is $10$. Anytime you add an even number to an odd number you get an odd number (even + odd = odd). So the blue light will always end up on odd.
Finally because red will always light up on even numbers and blue will always light up on odd they can never light up together. Using this rule we can tell that blue and yellow will never light up together because yellow lights up on even and blue lights up at odd.
McKenna generated new rules to find the rules which light up more than one bulb:

Now when attempting to find out when lights light up together I started by finding the lowest common multiple, LCM, of the slopes.
In the case of what you see on the right the LCM of the 2 slopes is $8$, now we need to find the y intercept for this equation. Now we come back to how we could right this equation as $8x - 5$ or $8x - 13$ or $8x - 21$. To find the $y$ intercept of this line we weed to find when the 2 lines meet. In this case it is easy because $4x - 1$ can be rewritten as $4x - 5$ and we don't have to rewrite the 2nd equation. Now that we know that the $y$ intercept is $-5$ and the slope is $8$ we can combine them to say that the equation for the blue and green lights to light up together $8x - 5$.
This also happens to be the equation of the green light so the blue light will always light up with the green light.
This method also works for finding 3 lights
Example:
Yellow =$ 7x - 5$
Blue =$5x - 1$
Green =$ 4x$
Yellow Blue Green = $140x + 144$
This almost works since $140$ is the lowest common mutliple of $7$, $5$ and $4$. However, $144$ (when $x=0$) will light up the blue and green lights, but not the yellow light.
Jessica and Sam also found some combined sequences:
$4n+1$ and $5m-2$ have a combined rule of $20k-7$
$10n+4$ and $3m-1$ have a combine rule of $30k+14$
$11n-5$ and $6m-5$ have a combined rule of $66k-5$
A pattern we can see for the combined rules is that to find the combined rules times the gradients together and then find the common differences in the new sequence.
Finally Herschel of the European School of Varese gave an insight into the method known as the Chinese Remainder Theorem:
We want to find a number that is part of two Arithmetic Progressions (APs): $an+b$ and $cn+d$. To put it another way, we are searching for a number $x$ that satisfies the congruences $x = b$ (mod $ a$) and $x = d$ (mod $c$). (The "mod $a$" part means that you look at the remainder on each side of the equation after dividing by "$a$".)
Finding this value of $x$ that will satisfy both equations and hence turn on both lights can be done using Chinese Remainder Theorem, which deals precisely with this problem - solving congruences.
For more information on the Chinese Remainder Theorem please look at this article.
Teachers' Resources
Why do this problem?
In this problem, students are presented with a mystery to be solved (what are the rules which govern the lights, and can all the lights be switched on at once?).
To satisfy their curiosity and explain the mystery, they will need to go in search of the information they require, and work in a systematic way in order to make sense of the results they gather.
The questions encourage students to think about the properties of numbers, including divisibility and remainders. It may help students gain a deeper understanding of linear sequences (and perhaps quadratic sequences, if they explore Level 2 and 3).
Possible approach
This printable worksheet may be useful: LightThinking.pdf
This problem follows on from Charlie's Delightful Machine, so we assume students have a strategy for determining the rules to switch individual Level 1 lights on.
Here are some questions you may wish to ask, to prepare students for what comes next:
What is special about a Level 1 rule where all the 'light on' numbers
- are odd?
- are even?
- are a mixture of odd and even?
- are all multiples of 3? Or 4? Or...
- have a last digit of 7?
"Did anyone find examples where two or more (level 1) lights switched on simultaneously?"
"Our challenge now is to determine how to turn on two (level 1) lights (or more) simultaneously, if we know the rules for each individual light."
If computers are available, students could work in pairs determining the rules for individual lights, then finding the rule for switching on pairs of lights simultaneously. Remind them of the importance of recording their findings to share with the class.
If computers are not available, students could explore pairs of linear sequences, searching for examples where two sequences have numbers in common.
One way they could record their work is by creating a table with sequence rules along the top and down the side, and indicating with a tick or a cross in each cell whether both lights could light up simultaneously. When appropriate, they could also indicate numbers which successfully switch on both lights.
Leave some time for the class to come together to share examples of rules where more than one light could be switched on simultaneously, and examples where it was impossible, together with their reasoning.
Key questions
What is true about any pair of rules where it is not possible to light up both lights?
If two sequences are described by the rules $an+b$ and $cn+d$, can you explain the conditions for determining whether the lights will ever switch on together?
Possible support
The problem Shifting Times Tables offers an introductory challenge for exploring linear sequences.
The problem Remainders explores some properties of numbers which could be useful when thinking about this problem.
Students could use a 100 square as a visual way to record sequences and see where (if) they coincide.
Possible extension
Some students may wish to use ideas of modular arithmetic to prove their findings; reading this article first may help.
