Primary proof?

Many people would suggest that proof has no place in primary mathematics classrooms. It needs to be too formal and rigorous, and young children find it difficult to follow and even harder to replicate for themselves. We would disagree and suggest that, on the contrary, ideas of proof need to be introduced to children when they are quite young so that they become comfortable with one of the central ideas in mathematics.

John Mason (1982) suggests that central to ideas of proof are notions of conviction and he suggests that there are three levels of this. Firstly we can consider whether we are convinced ourselves, secondly we can try to convince a friend and, the most rigorous level, we can try to convince an 'enemy'. This means that the argument should be strong enough to convince someone who is sceptical and can dispute any slightly under-justified steps in it. If these ideas are mentioned to children at quite a young age, we find that they are responsive to them and start to internalise them and to use them independently on their own initiative when they are engaged in reasoning about a mathematical problem.

We have already mentioned several aspects of proof in the previous paragraph. In their book Primary Questions and Prompts for Mathematical Thinking, the authors (2004) suggest that generalising, justifying and convincing are key elements of mathematical thinking and my own research (Back, 2004) suggests that classrooms in which teachers encourage pupils to participate in mathematical reasoning and argument are more likely to be successful in helping children to be enthusiastic mathematicians.

Many of the problems that we offer here on the NRICH website focus on looking for general rules by looking at a number of particular cases. Although this activity does not involve creating proofs as such, it is an important part of the process of proof. The theme of the June 2005 website is proof and we are offering several problems of this type.

Image

In Ring a Ring of Numbers , the interactivity allows pupils to enter their numbers into the boxes and displays the differences between the two boxes. This means that the focus of the pupils' activity is on the process of generalising about what is going on, rather than working out the answers. The generalisations that we are looking for here are about the sums and differences of odd and even numbers: an odd plus an odd makes an even, the difference between two odd numbers is even and so on. We are not asking for a proof as such but seeking to observe the general rules: the proof could follow later and might in fact be an appropriate extension to the question for slightly older children.

 

Image

Another problem that links with this is Make 37 which was published in October 2003. Once again there is no request for a proof but that is the natural solution of the problem. We have used this with a number of groups of children, and of adults, and the initial response is usually the same: people get stuck in and have a go. We would hate to spoil your enjoyment of the problem so we won't give the game away - do try it yourself before we proceed.

 

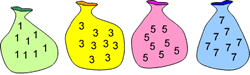
It hinges on what happens when you add two odd numbers. The proof would involve demonstrating that two odd numbers added together always give an even answer. What would we find acceptable as a proof at Key Stage 2 level? Here is one of the solutions that we put up on the website:





This is not the kind of proof one would expect from an adult or 'A' Level student but demonstrates a clearly reasoned and intelligible argument that convinces us certainly. In a recent article in 'Mathematics Teaching', Alf Coles (2005) talks about proofs that fail to convince even when one has followed every step of the logical path. He suggests that we need to offer children opportunities to gain insights into the mathematical contexts surrounding the proof before we can expect them to gain a thorough understanding and ownership of the proof itself. We would like to suggest that by offering children the opportunity to produce convincing arguments in writing or speech like the one above we will familiarise them with the process of creating proof so that the shifts to more formal expressions of proofs will come more easily later.

Several kinds of mathematical proof seem to be appropriate for introduction to young children. Possibly simplest is proof by exhaustion - only we have to be careful to choose problems that won't generate data that proves too exhausting! An example of this that we think works is the problem Crossings from the June 2005 website.

Image

To start with we have an investigation based on ideas about parallel lines and we move quickly into collecting data. How do we know that we have found all the possibilities for each number of sticks? We will need arguments based on the systems we have adopted for finding them and this will require data handling skills as well as being organised and systematic in our approach. The third paragraph moves into higher numbers and eventually into general number and algebra so should be a challenge to a lot of children even though the initial setting will be accessible to most.

 

Hopefully the experience of dealing with something that is initially straightforward will lead children into offering us a proof that makes sense to them and will convince us.

We look forward to receiving your children's proofs on the website.

References:

This article also appears in Primary Mathematics, a journal published by The Mathematical Association .