In July 2005 the NRICH website based a large number of its monthly problems around an interactive circular geoboard environment inspired by the ideas of Geoff Faux (1). That month's publication, based around an exploratory environment, reflects one of the ways in which the NRICH project is developing and changing its focus. In the past, the majority of problems were written so that they
could be used as a vehicle for consolidating and/or applying knowledge in a range of contexts. We wish our pupils to be proficient and confident in solving problems of this type and we will continue to offer such challenges. Over the last year or so we have also started to include problems that offer opportunities to learn new mathematics. Interactive environments, like Geoboards, can act as a
focus for such learning.
These types of interactivities have great potential as a resource in their own right, enabling problem posing by their users, as well as being used in conjunction with the problems we offer on the site. In this article we discuss what we hoped for when we published the environment and our vision for the future in terms of the creation and use of similar learning contexts (2) .
There are three major ways in which we imagine the environment and problems being used by teachers, and we list them here in order of the level of independence:
- firstly, using each problem independently as a focus for a lesson;
- secondly, selecting problems to tell a story and introduce some of the geometry of a circle over a period of time;
- thirdly, using the environment as a stimulus for posing your own (or your pupils') problems and supporting pupils' understanding of the properties of a circle.
The idea of teachers and pupils posing their own questions is the aspect of environments which we find most exciting, and it is interesting to note that when one of us recently used the material in a classroom this is exactly what happened. In this article we will describe the properties of the environment and discuss some of the problems in a little more detail. Finally, we will talk about
our experience of using the environment in a classroom.
The environment and some of the decisions we made
In creating the environment we made a number of decisions; most important was that the environment should be flexible enough to enable pupils and teachers to explore it and pose their own questions, not just use it as a means of tackling the problems we set on the site that month. That is, the environment should be a useful tool for teachers to use in the classroom on its own.
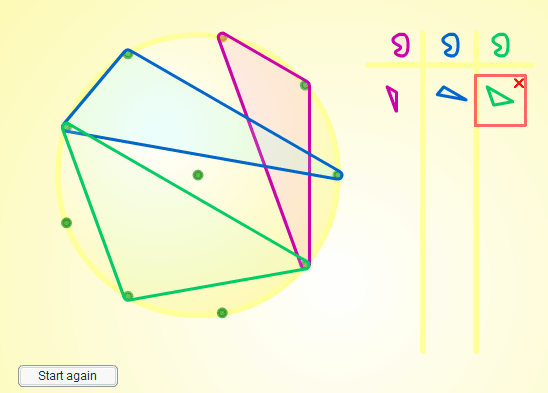
We wanted a means of recording what users had done, so in all cases, the environment has different coloured "rubber bands", and stores the shapes created in a simple table. We wanted to offer the flexibility to change the number of points around the circle so that it was possible to make conjectures based on a number of cases and then test generalisations. So in the general environment users
can change the number of pegs on the circumference of the circle and decide whether to include a peg in the centre (see figure 1).
Figure 1
For each of the problems on the site the environment was set up with a particular starting point in mind (eg a circular geoboard with ten pegs: nine around the edge and one in the middle). Downloadable sheets with different numbers of pegs are also available on the site. Of course, a set of nine-point plastic geoboards for hands-on experimentation would also be a great advantage.
How could the environment support teaching and learning?
So, once we had the environment what did we do with it? We wanted to pose questions that might lead the user to learning some new mathematics. What mathematics could potentially emerge? Having considered some problems as useful starting points, we looked at the numeracy framework (DfEE, 2001) and the mathematics national curriculum (DfEE and QCA, 1999) and were able to identify mathematical
content from each of years 2 to 12. Examples are
Nine-pin Triangles (3), Triangle Pin-Down (4), Subtended Angles (5), and
Pegboard Quads (6).
What this demonstrates is the flexibility of this environment, which can be used at a very wide variety of levels and with a variety of outcomes. Although we have given references to national curriculum and framework documents, it is perfectly possible that pupils will be working at all these levels in a mixed ability class. The environment also offers the potential to be a far more
stimulating and engaging way in which to learn circle theorems than the usual ones (see also Andrews, 2002).
Using the environment in the ways described above opens the possibility of learning mathematics through problem solving. Such environments also allow pupils to start from levels of understanding with which they feel comfortable.
How did the environment work in practice?
We recently led a two-hour session with pupils who had access to sheets with nine-point circles and plain circles (to which any number of points could be added) and a computer and data projector for using the interactivity. The session started with pupils being asked to consider this task:
How many different isosceles triangles can you draw on a nine-point circle containing one vertex at the centre? Calculate the size of their angles.
Pupils were asked to work on their own for several minutes before sharing their ideas with each other and/or the rest of their group, with some time given to questions that sought to clarify the problem, such as "What do you mean by different?"
The groups worked at quite different paces and took different routes, with one group extending their work to find the number of different isosceles triangles in a circle with any number of points and the sizes of the angles in those triangles, developing general rules in each case. This came as quite a surprise, as the question had seemed a fairly closed one and represented a starter to lead
into the rest of the session but also gave us lots of feedback on the "comfort zones" of pupils in the group. Some needed to spend quite some time convincing themselves that all the triangles were isosceles and that there were a very limited number of different ones; others quickly generated a general rule.
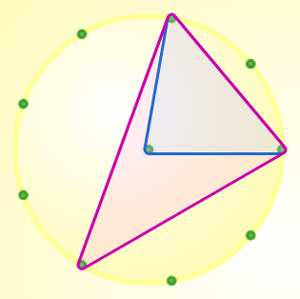
It was intended that the work on isosceles triangles with a vertex at the centre would lead naturally into considering the number of different triangles with all three vertices on the circumference of the circle and to calculating the sizes of their angles (without recourse to circle theorems, which they did not know). For a few, the knowledge gained concerning isosceles triangles was
brought to bear on the new problem without prompting; for some a diagram of a triangle with an isosceles triangle imposed on it (figure 2) was enough to make the connection; and for others a gentle nudge about using what they had already found was helpful. There were also two contrasting approaches to the new challenge. Some pupils immediately drew a triangle and, after some discussion,
constructed isosceles triangles and used them to calculate angles. Other groups became engaged in ensuring that they could find all the triangles first, with some of them wanting to generalise the rule for the number of triangles for any point-circle and comparing their findings with those for the isosceles triangles.
Figure 2
The original intention had been to move the pupils on to finding the angles of the circumscribed triangles, to look for relationships and to try to explain them. The two relationships that we had anticipated might emerge were that angles subtended by the same arc are equal and that the angle subtended by an arc at the centre is twice the angle subtended by the same arc at the circumference.
This would require a systematic search for patterns and relationships. For example, to ensure that they had found all the triangles they might need to draw them in an ordered way, starting with one side formed by joining two adjacent points, then two points one point apart and so on. Again, pupils worked at different paces and developed slightly different lines of inquiry, all of which appeared
to be helping pupils to establish the groundwork for the identification of a general rule and then an explanation of why it might be the case, possibly by first looking at circles with different numbers of points. The impressive thing was the amount of problem posing that was going on and the evidence that pupils were working from their own understandings and building on them with confidence. The
session ended with a discussion of strategies that might lead to identifying and describing relationships.
The next time we meet, we will continue the journey, probably moving on to identifying, generalising and justifying the angle properties of triangles in a circle and looking at the special case of the angle in a semicircle and angles of a cyclic quadrilateral. Now the latter does not feel like an extension of the work, just a natural progression.
What was clear was that the environment and findings were making sense to many of the pupils who had the freedom to start off from a point where they felt comfortable.
And where to next?
We will continue to develop environments and offer some ideas for problems at a range of levels, but one of our main hopes is that teachers will make them their own, encouraging pupils to pose their own questions alongside the ones suggested. A completely open starter might be "Investigate this environment and describe and justify what you discover."
We would welcome ideas for more environments.
References
- Andrews, P. (2002) Angle measurement: an opportunity for equity, Mathematics in School, 31,5
- DfEE (2001) Key Stage 3 National Strategy: Framework for teaching mathematics: years 7, 8 and 9
- DfEE and QCA (1999) Mathematics: The National Curriculum for England and Wales
Notes
- Real boards (18.5 cm in diameter, moulded in crystal clear ABS and suitable for using on an OHP) are available, together with a teacher's guide, from Geoff Faux at Education Initiatives .
- You can find most of the problems and the environment itself by searching for "geoboard".
- Framework reference: KS1, Y2: make and describe shapes; sort shapes and describe some of their features
- Framework reference: KS2, Y5: properties of numbers (factors and multiples); recognise properties of shapes
- Framework reference: KS3, Y7: Geometrical reasoning: lines, angles and shapes
- National curriculum reference: higher: properties of triangles and other rectilinear shapes; properties of circles
- For those of you who are interested, the mathematics behind the programming of the environment and some of the issues that needed to be addressed was also published on the NRICH website in July 2005.