Age
7 to 14
| Article by
Lyndon Baker
 | Published

Bands and Bridges: Bringing topology back



The fascinating model described in this article was created by Augustus Mobius (1790 - 1868), a German mathematician and astronomer.

Here is a limerick describing the properties of the Mobius band:

"A mathematician once confided

Old Mobius' band is always one sided

If you want a good laugh

Cut the band in half

Notice, it stays in one piece when divided.''

(Source unknown)

You need:

$\bullet$ four long strips of paper, strips of A3 about 30mm wide are ideal.

$\bullet$ to draw in a centre line along each strip.
Bands and Bridges: Bringing topology back
$\bullet$ some glue or sellotape and a pair of scissors.
 
Model A : Take a strip and glue the ends together.
 
Model B : Take a strip and at one end make a half twist ($180^{\circ}$). Glue the ends together.
 
Model C : Take a strip, at one end make a full twist ($360^{\circ}$). Glue the ends together.
 
Model D : Take a strip, at one end make three half twists ($540^{\circ}$). Glue the ends together.
 
 
Take each model in turn. Examine it carefully. Predict what will happen when a cut is made along the centre line.
 
Cut your models and record your results in the table below:
 
MODEL NO. OF TWISTS CUTTING PRODUCES DESCRIPTION
A 0 2 separate strips half width/same length
B 1/2    
C 1    
D 1 1/2    
 
 
Can you predict what `shape' results for any number of half twists?
 
What about 6 half twists? 10 half twists?
 
You might like to investigate models based on a Mobius strip which has two or more lines to cut along.
Bands and Bridges: Bringing topology back
What next? ...


This work on the Mobius band can be followed by an investigation into Euler's law.


Leonhard Euler (1707 - 1783), was a Swiss mathematician who is possibly best remembered for a rule he found that worked equally well with networks and polyhedra.


A network is a collection of vertices (dots) connected by arcs (lines) that create regions (spaces) in between.


Bands and Bridges: Bringing topology back


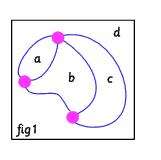
FIGURE NODES REGIONS ARCS
1 3 4 5
2      
3      
4      
5      
 


This network has 3 nodes, 5 arcs and 4 regions. The outside is counted also.

Study the networks below and complete the table.

 
Bands and Bridges: Bringing topology back


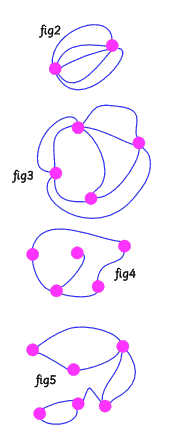
What do you notice about the information in this table?

Does you observation always work?

Can you find a network which does not fit in with your conclusions?

Would your observations still hold true if you had drawn the networks above on a ball or an inner-tube?

Have a look at The Bridges of Koenigsburg if you'd like to try another knotty problem.