Dicing with numbers
Problem
In how many ways can you arrange three dice side by side on a surface so that the sum of the numbers on each of the four faces (top, bottom, front and back) is equal?
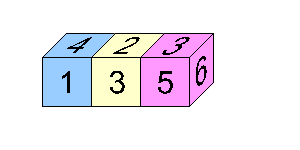
What can you say about rows of four, five, six, ...... dice?
Getting Started
Student Solutions
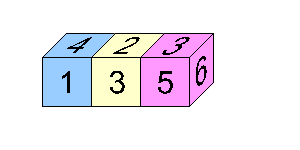
Originally no correct solutions were received for this problem in the month after its publication. It is a nice one to think about and is not too taxing if you know just a little about the properties of opposite numbers on a die.
Almost simultaneously, solutions to this toughnut were received from Cameron who is home-schooled (whose solution is given below) and Joel of Raffles Junior College.
Three dice cannot be arranged in any way that makes the sum of the top dots equal the sums of the front, back, and bottom dots.
There are six faces on a die: 1, 2, 3, 4, 5, and 6. These total
to 21.
Three dice have a total of 63 dots. When three dice are arranged in
a line, and we are concerned with only the top, bottom, front, and
back sides, the end faces and hidden faces do not count.
If we were to pull apart the row of dice so we could see the hidden faces, we would see that each hidden face is opposite from either another hidden face or an end.
Opposite faces of a die always total 7, so the two opposite
faces of each die that we aren't concerned with total 7 each,
therefore 7+7+7=21.
The remaining dots (top, front, bottom, back) equal 63 (total of
all faces) - 21 (total of faces we aren't dealing with) = 42.
Since 1/4 of these dots must be on the front, 1/4 on the back, 1/4 on the top, and 1/4 on the bottom, we can divide 42 by 4 to see how many dots are facing one direction. 42 ÷ 4 = 10.5, which cannot make a solution because there are no half dots on regular dice.
Therefore 3 dice will never satisfy the requirements.
Using the same formula (n = number of dice, t = total: 14n ÷ 4 = t, t must be an integer), only even numbers of dice can be arranged so it is possible that sum of dots on top faces = sum of dots on bottom faces = sum of dots on front faces = sum of dots on back faces.