Some thoughts on teaching about area

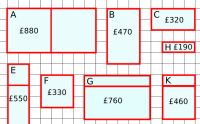
One of the most common problems that arises when secondary school students work on problems about area is the confusion between area and perimeter. Looking at a common textbook treatment of area and permiter suggests why this confusion might arise: many textbooks introduce perimeter and area separately, but on consecutive pages of the book, using exactly the same diagrams and examples, often looking at areas of rectangles. A child takes away from this a formula for area (length multiplied by width) and a formula for perimeter ($2l + 2w$) having worked mainly with rectangles.

Image

Perhaps a better approach would be to work with the concepts of area and perimeter together. By looking conceptually at the two quantities, it becomes clearer that they measure two different properties of a shape, and the names 'area' and 'perimeter' can be hung onto the concepts once the student has a need of names to refer to them. Take a look at the problem Warmsnug Double Glazing. A student does not need a formula for calculating area or perimeter in order to appreciate that some of the windows need more glass than others, and some need more frame than others. To solve the problem, the concepts of area and perimeter need to be present, but the names do not.

 

Image

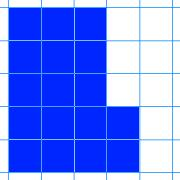
Another common misconception among students with a shaky grasp of area and perimeter is the notion that the two increase together, that is, the greater the area the greater the perimeter and vice versa. Changing Areas, Changing Perimeters directly challenges that notion by provoking students to think about the two quantities together and to vary one while keeping the other the same.

Area is an important concept for older students too. When learning about calculus, the idea of integration as area becomes very useful for applications. Many students have a superficial understanding of differentiation based on applying a rule ($x^n$ differentiates to give $nx^{n-1}$) and then learn integration as the inverse of differentiation. In the same way that learning about area and perimeter separately, as rules to be memorised, leads to students confusing the two concepts, many markers of A level papers will have seen students integrating rather than differentiating, or vice versa, because the students are following a rule rather than showing their understanding of a concept.

Image

Integration Matcher requires no understanding of integration or differentiation, as the cards can be handed out with the explanation that some of the graphs show the area under the curve of some of the other graphs, and students can be invited to match them. This helps students to develop a conceptual understanding of integration as area that can then be applied to problems. Of course, the same set of cards could be used to encourage students to explore graphs of the gradient as a precursor to differentiation!

Research shows that conceptual understanding leads to students retaining knowledge much better than rote learning of formulae. We hope that working on some of the tasks identified above will help students to develop the important concepts that will lead to better understanding as well as examination success!